ここは環状線・地下鉄「玉造」が最寄りの駅になるビリヤードとダーツのお店「セクションエイト」。
私は初めてといっていいぐらい、ダーツもビリヤードもしたことがない。やったことはあるが遥か遠い昔の記憶。
このセクションエイトのオーナーの夫人が、仕事仲間だったということで、その仲間たちと訪れた。道路に面している二面がガラス張りという、大変開放感のあるお店。
土曜日の午後に訪れたが、中高年の人たちがビリヤードを楽しみ、若者のグループがダーツに興じていた。
さて、せっかくダーツをするのだからちょっと勉強になることを、と思っていたら前回紹介した本、「直感を裏切る数学」にダーツの事が書いてあった。本を元に勉強したことを紹介してみよう。
ダーツといえば上の写真や下の絵のようにダーツボードに刺さった矢の位置で得点が決まる。
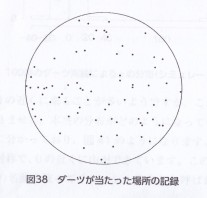
ダーツボードに当たった点だけを考えることにする。線の上でも当たったと考える。
そこでダーツが中心からどの方向に外れたかを見ることにする。
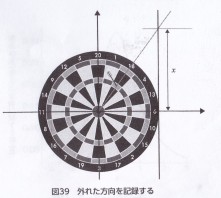
左の図のように、中心とダーツが当たった場所を通る直線を引いて、図のような垂直線に交わる横軸までの距離(高さ)をxとして記録していく。
このとき、xの値がマイナス無限大からプラス無限大までにする、というのがポイントになる。
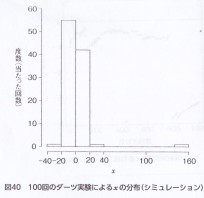
100回のシュミレーションの結果をヒストグラムにしたものが次の図。
ヒストグラムというのは、この場合では、横軸にxの範囲を20ずつまとめた区切りを入れ、縦軸にその範囲におさまった回数をとったグラフのこと。
このグラフを見てみると、xが0の近くに来ることが多いように見える。
ただ160付近に極端に離れた場所にグラフの山があることに注意しておこう。
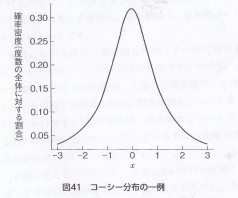
実は本当の分布については、理論的にわかっていて、左のようなグラフになる。左右対称で、0の近くに大きな山ができている。
統計でよくみる正規分布によく似ているが違う。
この分布は、発見者の名前をとって「コーシー分布」と呼ばれているもの。
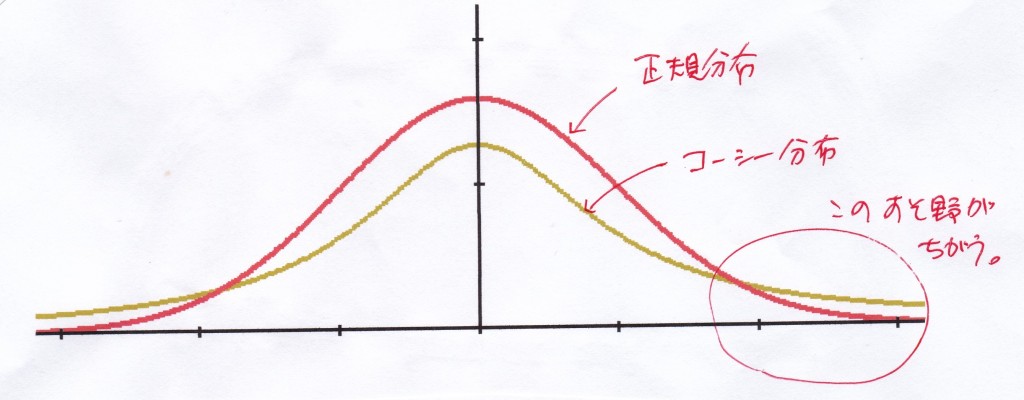
「すそ野」が高さの違いに着目しておこう。
正規分布なら平均は0、となるが、実はコーシー分布には「平均が存在しない」のである。
ダーツを投げる実験をさらに続けることにする。
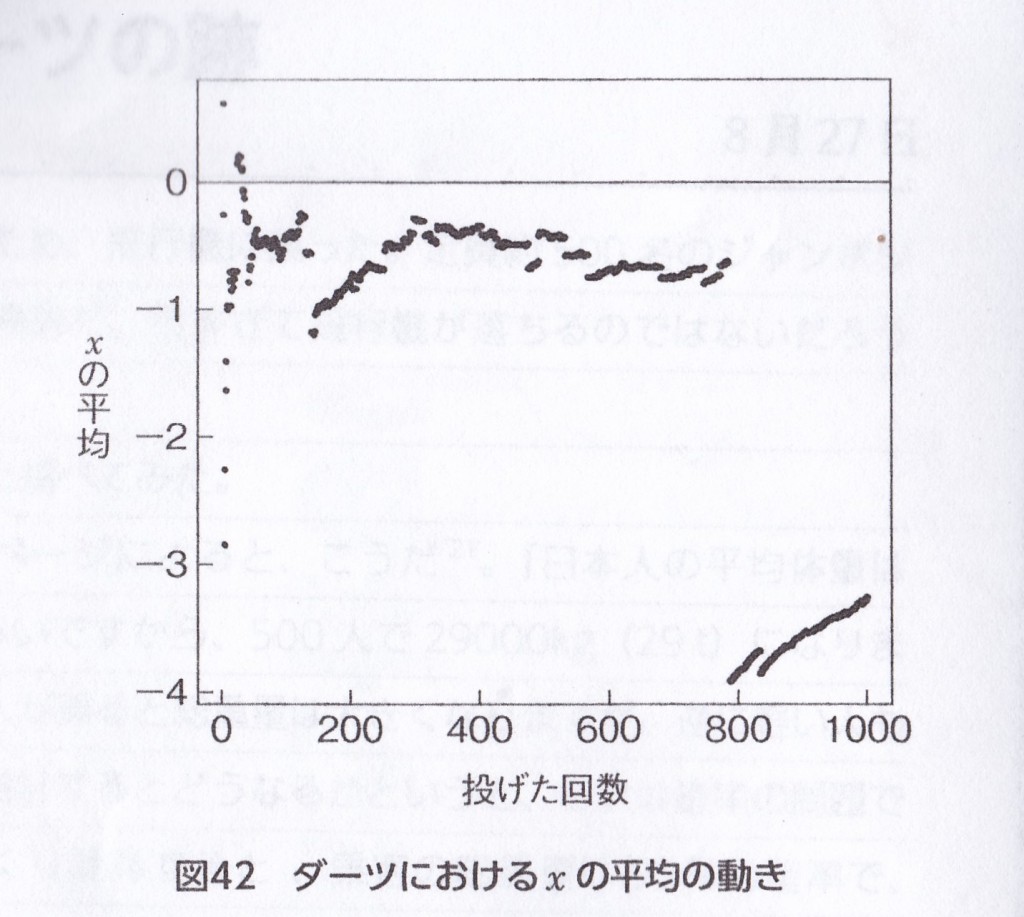
1000回投げる場合をシュミレーションしてみると、
0に近づくような動きも見られるが、ときどきドーンと下がるような動きがあって、0から大きくはずれる場合が観測される。
私もダーツを投げると、ときどき思いもかけずに投げ損じて、ダーツボードから外れてしまったことが何回かあった。これである、この動きが平均0を大きく引き下げていると考えられる。
サイコロを何千回なげると、それは平均してみると同じ数字がでる確率が六分の一、という場合と全く違った事象なのである。
極端に0から外れた値が出るのが、「それほど稀ではない」というのがコーシー分布の特徴と言われている。
「標本平均は、標本の大きさが大きくなればなるほど真の平均に近づいてくる」という大数の法則があるが、ダーツの場合は成り立たないのである。
大数の法則が成り立つには、大きな前提がある。それは「真の平均が存在する」という前提があってのことである。ところがダーツの分布にはこの前提がないのである。
コーシー分布の典型的な例としてあげられるのが「ガラスの破片」である。
「岩石に衝撃を与えて粉砕するとその破片の大きさの分布はべき級数になることが知られています(注 コーシー分布もべき級数である)。ガラスのコップを固い床に落として割った時にできる破片も同じです。大きな破片はほんの数個で、中くらいの破片はかなりの数になり、小さな破片は無数にあります。眼に見えないような小さな破片の数はさらに多くて、顕微鏡で拡大してみても同じような分布が観察されます。顕微鏡でも見えないくらいのホコリのような破片の数が最も多いので、1つずつの破片の大きさの平均値を求めると、事実上ゼロになってしまうのです。破片の大きさの標準偏差を計算すると、今度は少数の大きな破片の寄与が無視できなくなり、非常に大きな値になります。何桁も大きさの違う破片が混在しているから、ゆらぎの幅を表す標準偏差が大きな値になるのは当然といえるでしょう(「経済物理学の発見」より)。」
ときどき出現する極端な例が、標本平均を大きく変えてしまうのがコーシー分布の特徴なのだ。
地震の発生も平均で計算することはできない、経済の株価の動きも平均によって予測することができない。この世の中の実際の世界は、標準偏差で平均値が求められるような世界ではなくて、コーシー分布で表されるダーツの世界がこの世の中を表しているのかもしれない。
明るくて健康的なビリヤードとダーツのお店「セクションエイト」のオーナーと、若くて美人のオーナー夫人の親切な指導で、ビリヤードとダーツの腕が上がりそうな予感。でもこの予感もコーシー分布かもしれないなあ。