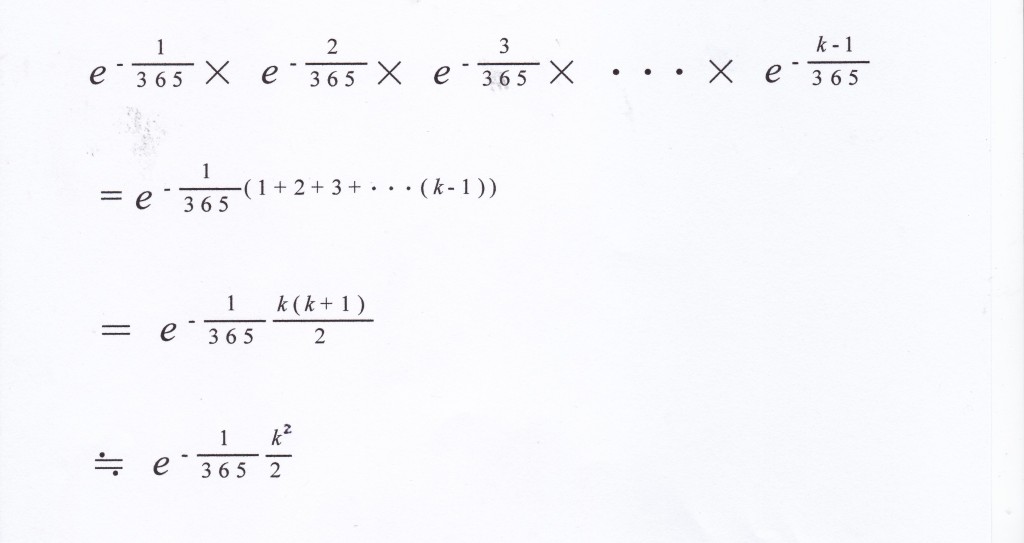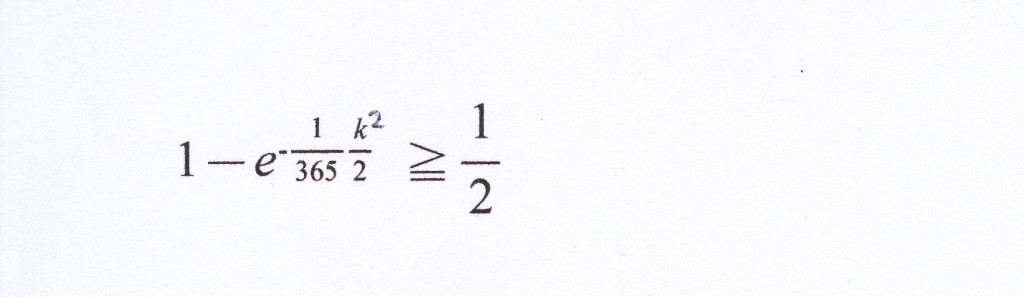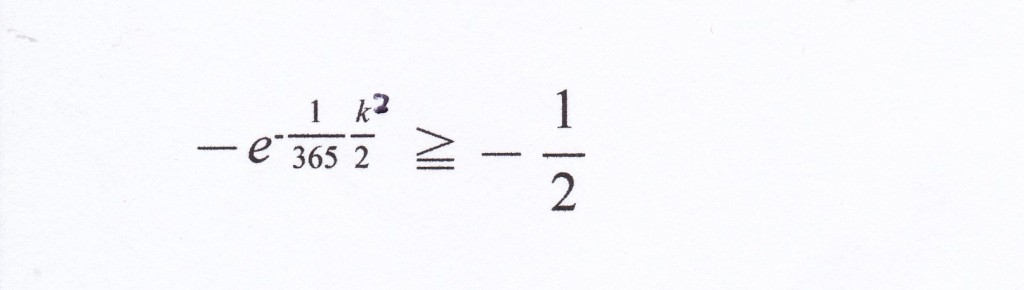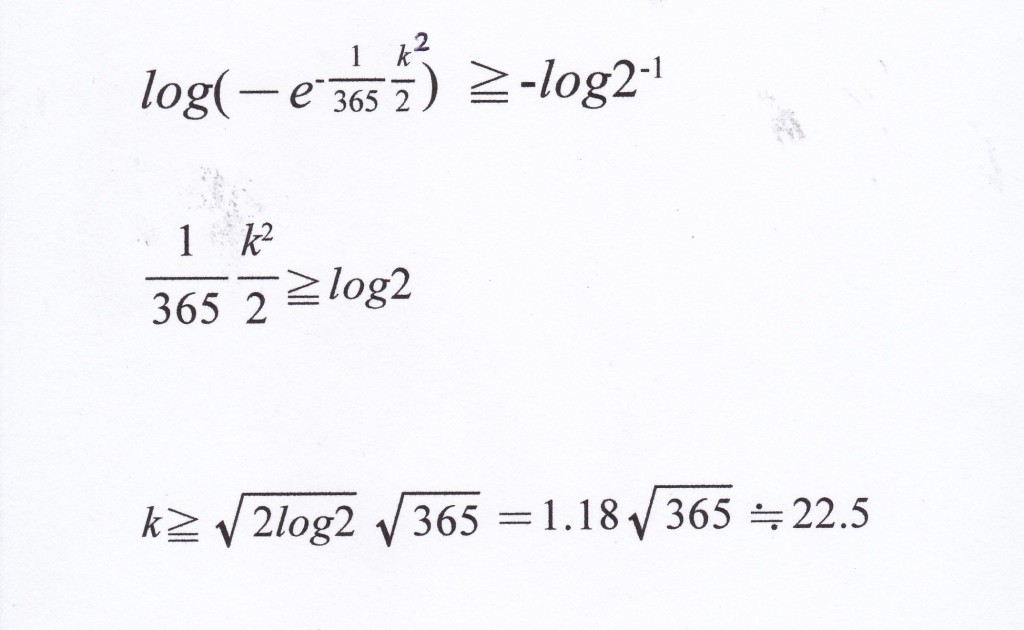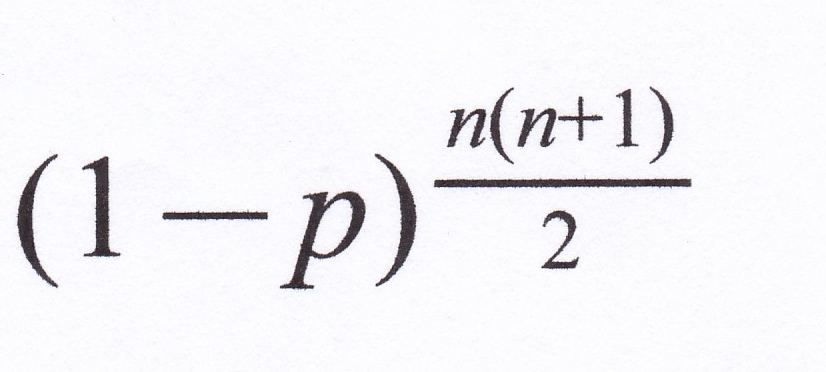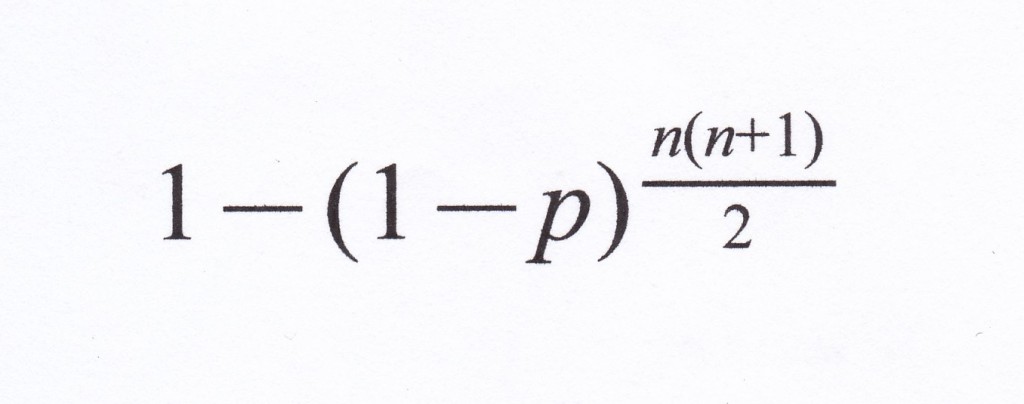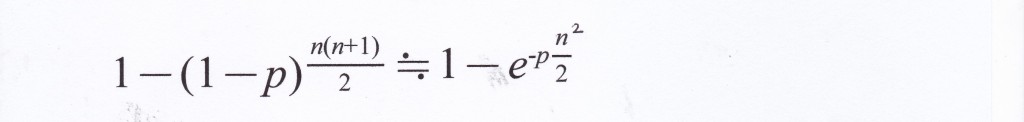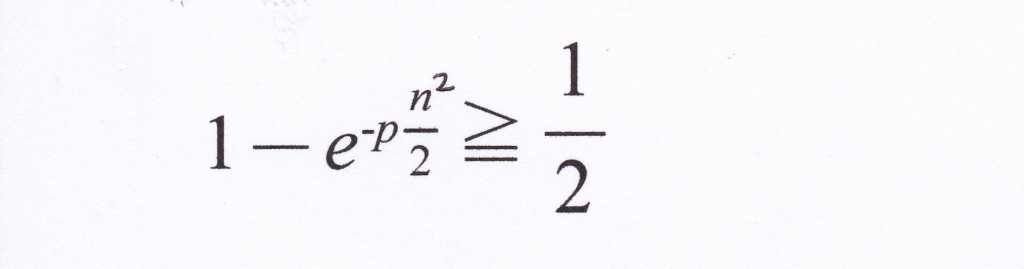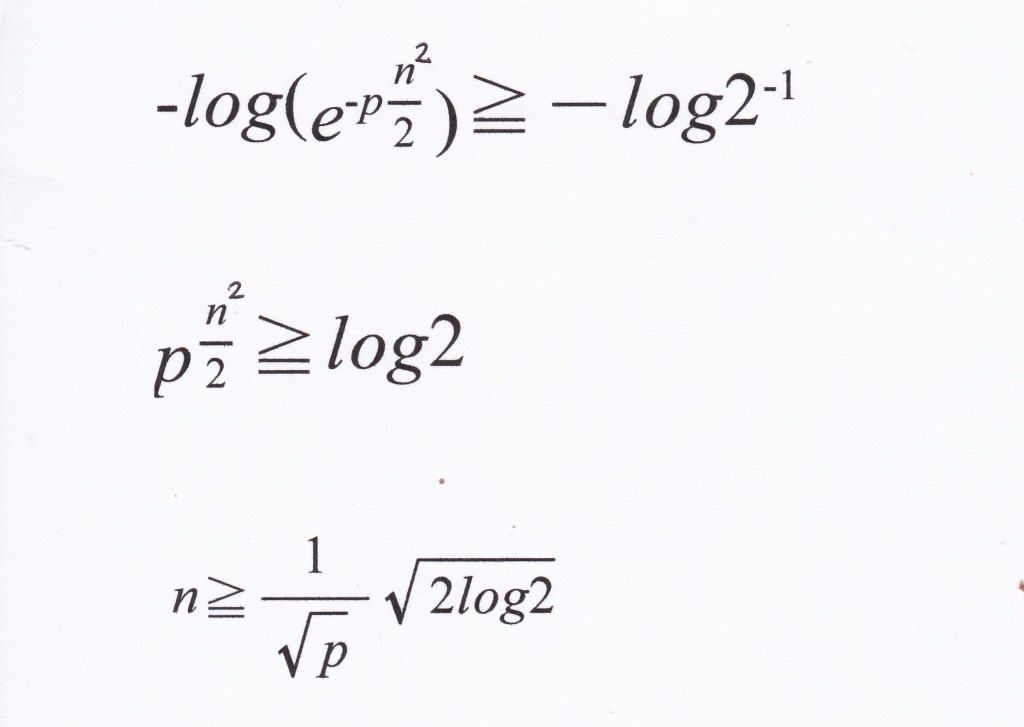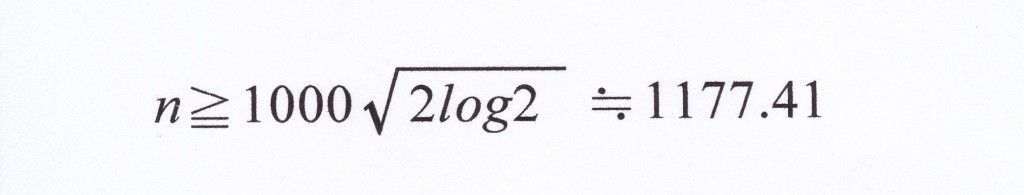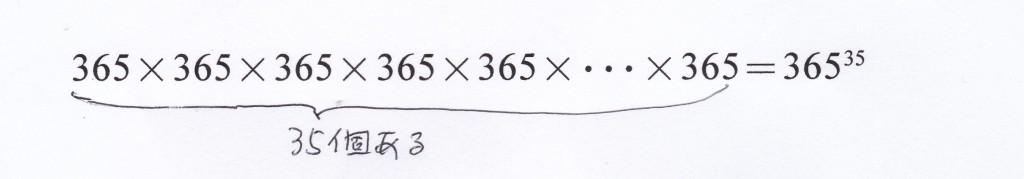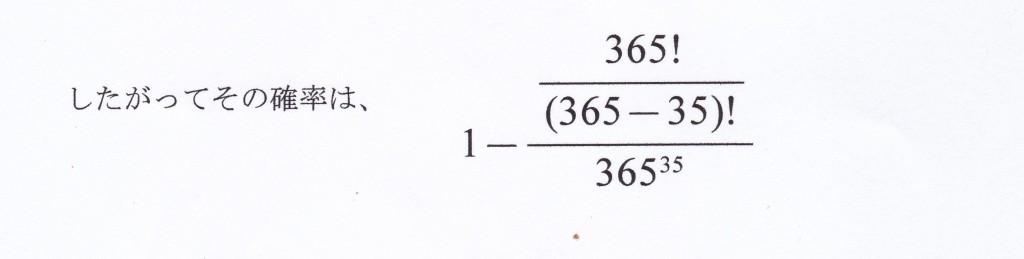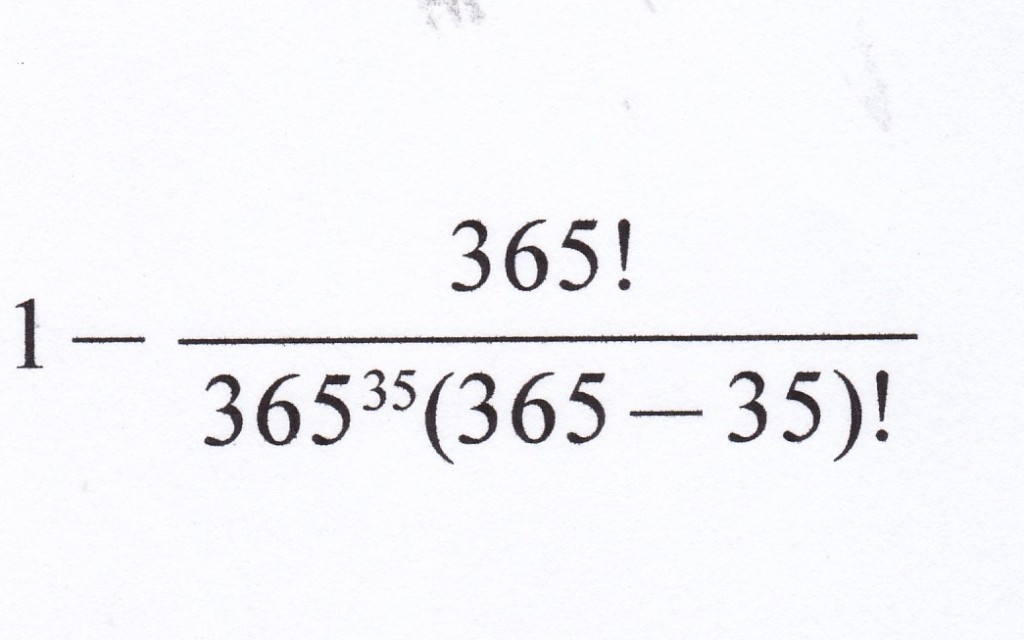誕生日が同じだと運命の出会い、と思うが、それはどれくらいの人数の集団がいるかということに関係することは理解しやすい。365人いれば自分と同じ誕生日の人がいても不思議ではない、と思うのが人の気持ち。
でもこんな男女の出会いならなにも危機はないのだが、人数が多くなると思いもかけない心配事が出てくる。以前紹介した「直感を裏切る数学」にそって説明をしてみよう。
ここで、一般的な式を求めるために、
この式を次の近似式をもとに簡略化する。
ここまで計算したのは、誕生日が一致しない確率だから、一致する確率は
「1引く一致しない確率」であることを利用して計算する。
それが、50%、2分の1を越える場合を考えと、
左の式を計算すればよい。
ここで両辺の対数をとる。 (対数の底をeとする自然対数)
自然対数の場合は、
log e = 1
である。
また
1/2 = 2のマイナス1乗
であることを利用して計算している。
以上のことより、23人いれば誕生日が一致する確率は5割を越えることが分かる。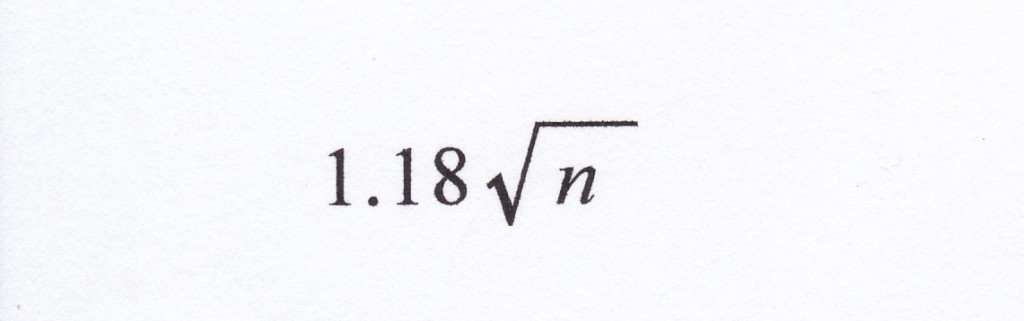
この関係式を一般化したものが左の式である。一般にn通りある場合、およそ5割になるには左の式の値を利用すればよい。
たとえば誕生月が同じ確率は、上の式にn=12を代入して計算すればよい。結果は
約4.1で、5人いれば同じ誕生月の人がいる確率は5割ということで、これはなんなくそうかなあという実感に合う。
さて、ここまでの考え方を利用してさらに一歩すすめてみる。
ペアの数を考えてみる
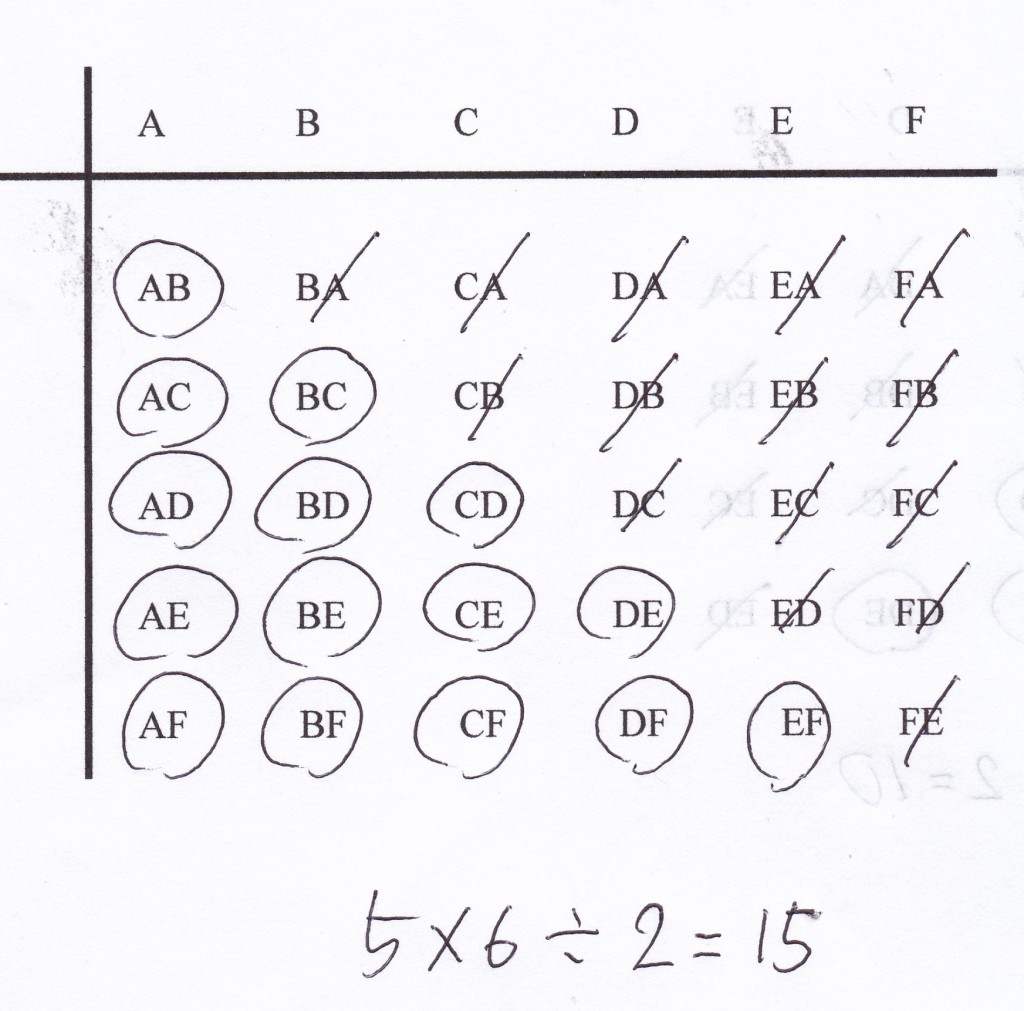
A、B、C、D、E、Fの6人がいるとする。
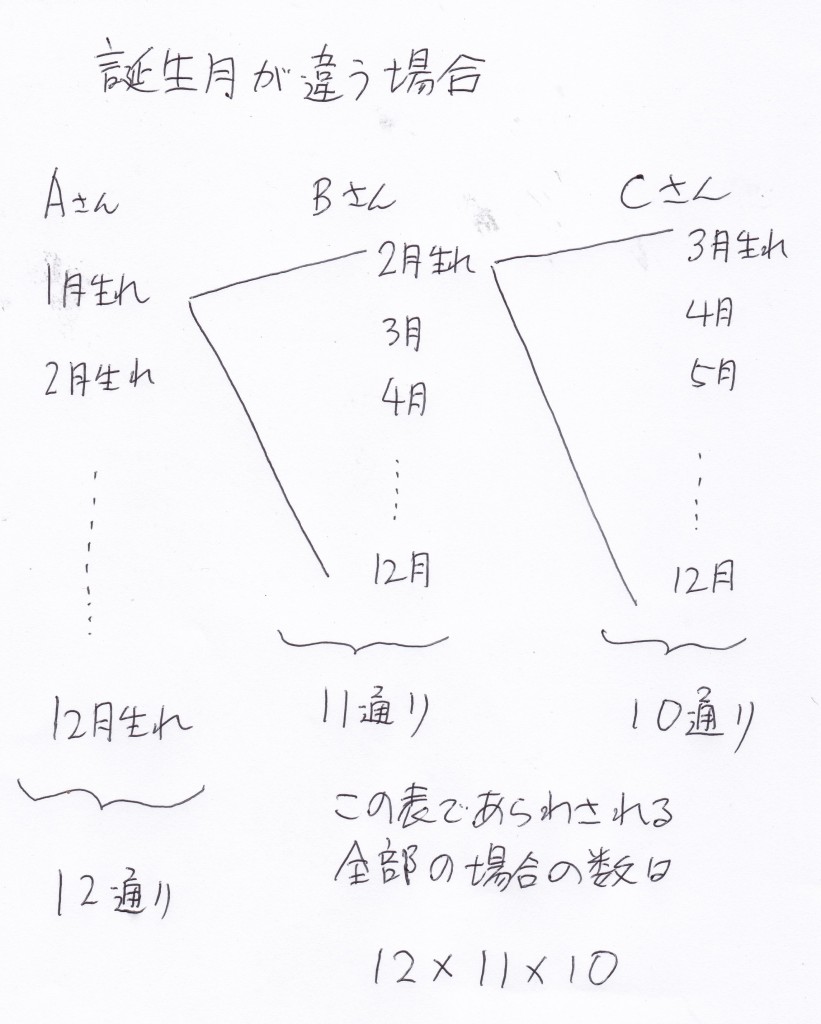
Aをもとにペアを作ってみると、下の図のようになる。
最初にABという組み合わせを考えてFまでの組み合わせを考えると、5✕6の
30通りできる。
ただAB、BAと同じ組み合わせがあるのでその分を考えると、2で割ればいいとこがわかる。
6人いれば、ペアの組み合わせが15通りあるということである。
35人いれば
35✕34➗2=595
通りあることがわかる。
595のペアがいれば、同じ誕生日の組み合わせはかなりあるのでは?と予想される。
35人では自分と同じ誕生日の人がいる確率は少なかったけれど、「誰かと誰かの誕生日が同じになる確率は高くなる」。これが「誕生日のペアが成立する確率は高い」ことの本質である。
誕生日、血液型、DNAiなど自分であることを証明するための方法はいくつもある。しかしそのデーター数が数100万単位だとすると、他人と同一視される確率は高くなっていくのではないか?そんな不安がでてくる。
他人と間違えられる危険率が100万分の1のときは?
他人との分類を精密にしていけば行くほど、エラーが出てくる確率が増えるのは予想できる。 Pitapaや銀行のカードでも、もう一度やり直してください、というエラーが出て、どうしたんだ?!と思う時があるように。
今ここで1つのペアにつき、他人受容(他人と間違えられる)確率をpとしよう。
p=1/1000000(100万分の1)のとき、
他人と間違えられない確率は、
1−p=0.999999
となり、ほとんど1だが、1よりほんの少し小さい値になる。
データの数をnとすると、ペアの数は
n(n+1)2
となる。
データベース全体で他人受容が起きない確率は、
となるので、
全体で
他人受容が起きる確率は全体の1から
この式の値を引けばいいことが分かる。
先ほどやったように、eを使って近似式に変形し、他人受容確率が50%をこえるのは何人の時か、同じような方法で計算してみよう。
log e = 1
1/2=2のマイナス1乗
を利用して計算する。
ここでp=1/1000000(100万分の1)を代入すると、
どちらも同じ結果が出てくる。
つまり、他人と自分が同一だと判定される確率が100万分の1であっても、
1180組ペアがあれば、同一人物であると判定されるペアが現れる確率は50%をこえる、というわけなのである。
これは大変なことである。
指紋やDNAは100%の確率で個人を特定できる、思っていたがとんでもないことなのだ。
この本によると、DNA鑑定は、DNAに含まれる全ての塩基配列を調べるわけではない。また警察白書によると同一のDNA型の出現頻度が4.7兆分の1と記されているが、和田俊憲「遺伝情報・DNA鑑定と刑事法」(慶應法学第18号(2011))という論文では「この確率を基にして、地球全体、あるいは日本全体で同一ペアが存在しない確率は極めて小さく、ほとんど0とみなせる」とある。つまり、DNA鑑定で、同一人物だと判定されるペアはほぼ確実にいるということなのだ。
実際にアメリカのメリーランド州で2007年1月に、3万人のデータの中で、他人なのにDNAの一致が実際にあったという資料も紹介されていた。
さきほどの4.7兆分の1という確率もあくまで理論的なものであり、実際にはもっと大きなものになるのかもしれない。
指紋やDNAの鑑定だけで他人と間違えられたり、事件に巻き込まれてはたまったものではない。
ブログでお世話になっている風見鶏さんから「病院では誕生日だけでなく、血液型も聞かれて本人確定をしています」とコメントがあった。
なるほど、大きな病院になればなるほどそういった工夫がいるのだと実感した。
バースデイパラドックス
私は「誕生日の確率から、危機が生じる」と感じたので、バーズデイクライシスと書いてきたが、統計の世界では「バースデイパラドックス」として以前から有名なことだそうだ。
「直感を裏切る数学」の作者の神永さんはこうしめくくっている。
「情報セキュリティの教科書には、バースデイパラドックスが必ず載っています。それには2つの意味があるでしょう。
ひとつは当然のことですが、情報セキュリティに携わる者が、絶対に理解しておかなくてはならない事実だということ。
そしてもうひとつは、日常的に数学に触れている者でさえ、正確に確率を把握するのは非常に難しいということです。
直感で「ざっくりこのくらい」と見積もるのではなく、きちんと数えあげることの重要性を示唆する話ではないでしょうか」。
単純に「誕生日が同じ人はどれくらいの確率でいるのだろう」という疑問からスタートしたが、バースデイパラドックスは統計の世界では必修のものだったのだ。
直感と実際のはざまは、思っている以上に大きな溝がある、ということがあるのだ。