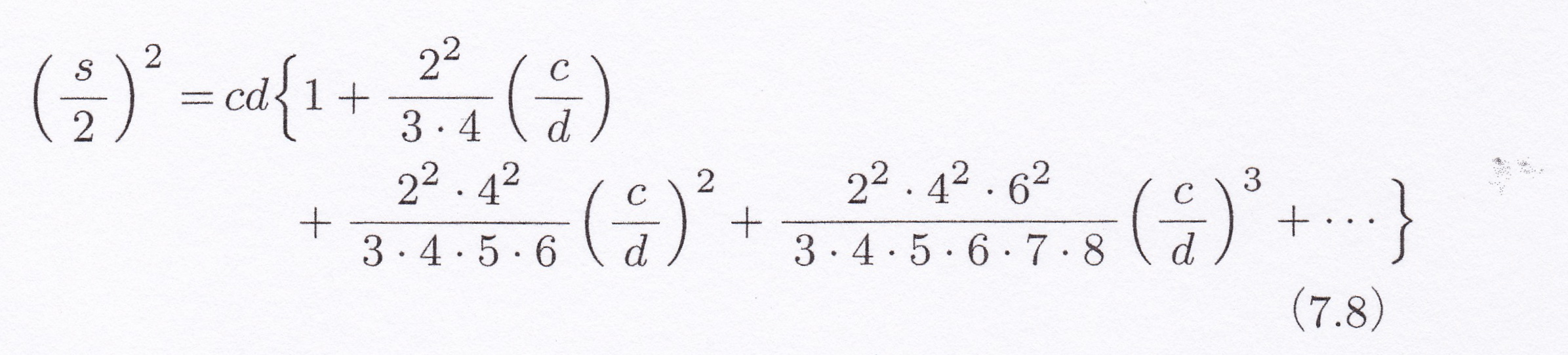小説「天地明察」を読み、映画も見た頃から、和算による円周率の計算に興味があり、何冊か本を読んできた。一番最近の本が岩波現代全書の「円周率が歩んだ道」(上野健爾著)。
この本はヨーロッパだけでなく中国やモンゴルでの円周率計算の歴史にも触れ、もちろん日本の和算の成果もきっちり書いてある。また、私の理解力ではまだまだついていけない16進数による円周率の計算の有効性から新しい数学への展望や、付録には「円周率が無理数であること」「円周率が超越数であること」の証明までのっている興味深い本。
私は和算による円周率の計算に興味があるので、そこの部分を実際にペンで計算しながら勉強のつもりで読んでいった。本と自分の計算とあわないところが出てきてまる一日ほど悩んだところがあった。それはこのページの最後の式。
少し円周率の歴史を振り返ってみよう。江戸時代も円周は直径のほぼ3.14倍ということは知られていた。それを精密に計算しようと江戸時代の和算家は努力した。
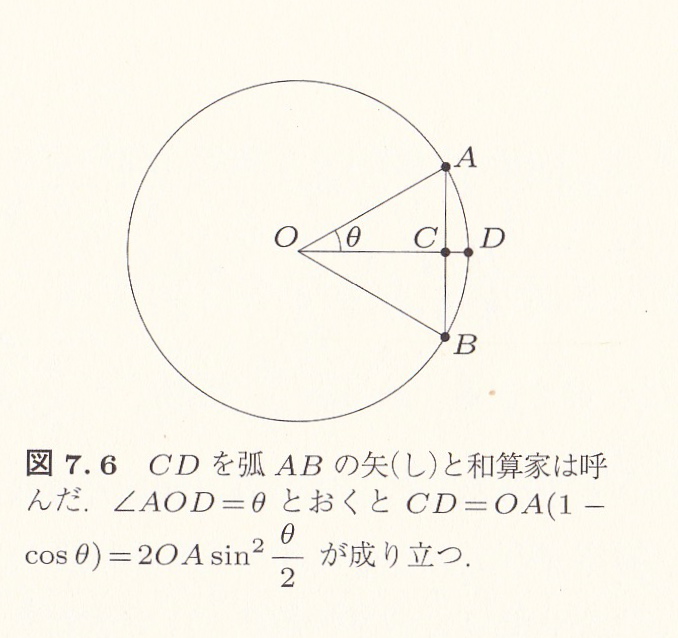
江戸時代の和算家が円周率の計算で利用した矢(し)について説明すると、弦と弧については現在の学校で習うものと同じ。
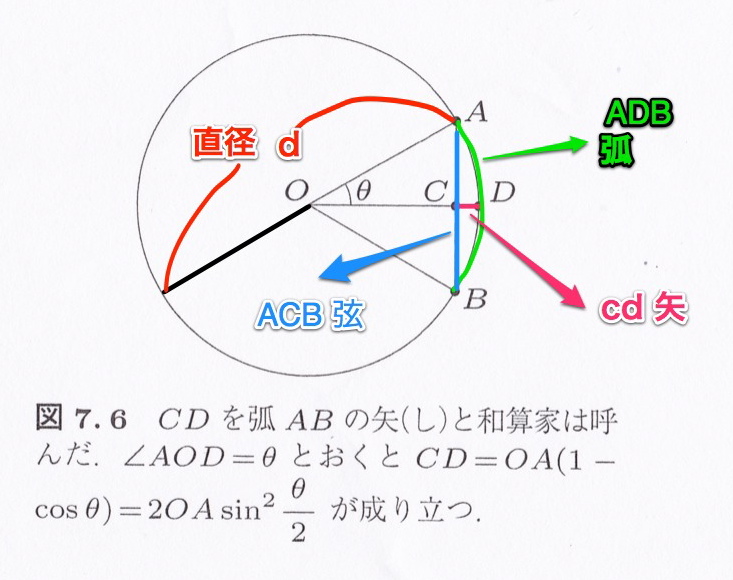
弧ADBを弓、ACBを弦(つる、ゲン)と見立てると、CDは弓の矢に見えてくる。それでCDを矢(し)と呼んだ。
和算家の建部賢弘は、弧ADBの長さを直径dと矢CDの長さを使って表すことを考えた。円弧の長さがわかれば円周がわかる。つまり「直径と円周の関係をあらわす式を見つけることができる」というふうに考えた。
その結果が上にある式(7.8) である。
ここで弧度法(ラディアン)を使い、三角関数の式に変形する。
弧ADBの長さをs 、角AOD=θ 、矢CD=c 、直径=d とすると下のように変形できる。
*この時の計算がp147の最後の式。ここに問題があるがそれは後で。

実はこの式はオイラーが1737年に発見した式だが、建部賢弘が1722年に著した本「綴術算経」に書かれており、このことにより建部はオイラーより早くにこの式を発見したと言われている。
ところで江戸時代に三角関数は使われていたのかという疑問が出る。なんと我が国での最初の三角関数表は建部賢弘の『算暦雑考』に記載されている。
ここでこの式を円周率を求める式に変形する。
このようにして円周率πをもとめる公式が導き出された。これが江戸時代の建部賢弘の考え方である。
この公式を求める途中の式の変形で、本文p149の最後の式がある。
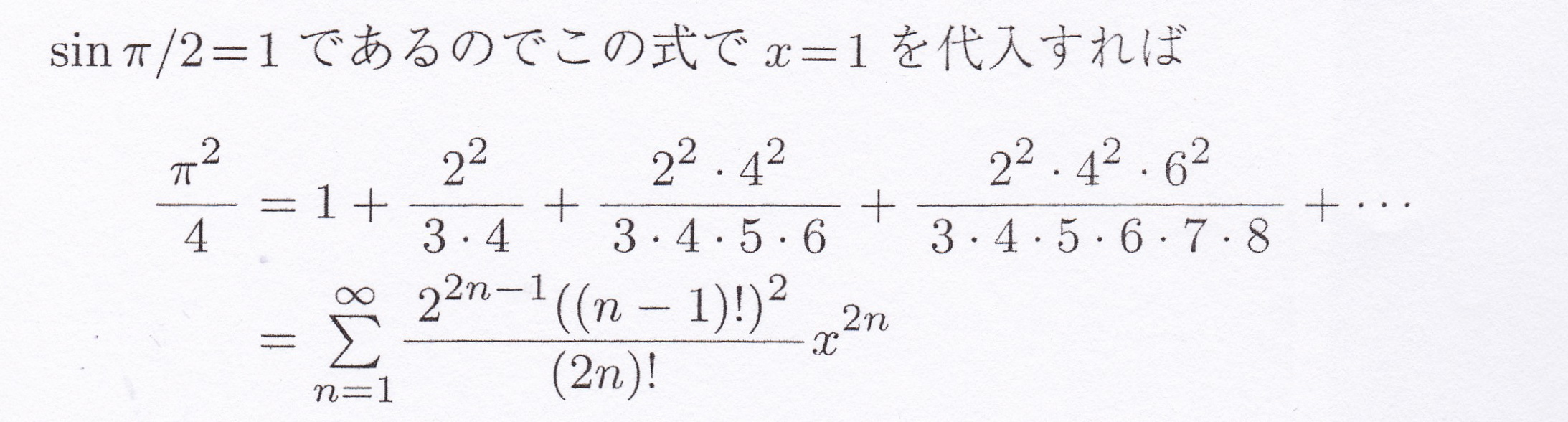
私はここでつまづいた。
半径=1/2*d
AD=1/2*s
だから弧度法を使うと
1/2*s=1/2*d*θ → s=d*θ
ここまではわかる。
次の式がおかしい。c=d – d*cosθ ではなく、
c=1/2*d – 1/2*d*cosθ
でなければならないはず。dは直径なのだから半径にするために1/2を掛ける必要がある。
c=1/2*d – 1/2*d*cosθ
c=1/2*d*(1 – cosθ)
*三角関数の半角・倍角の公式 cos2θ = 1 – 2sinθ*sinθ を使い、
1 – cosθ = 2sin(θ/2)*sin(θ/2) これを代入すると
c=1/2*d*(1 – cosθ) = 1/2*d*2sin(θ/2)*sin(θ/2)
c=d*sin(θ/2)*sin(θ/2)
となるはず。本のように
c=2d*sin(θ/2)*sin(θ/2) とはならない。
この式をもとに計算してもこの本の次ページの式にならない。
どうしてだろうと悩んだ挙句、係数2が不必要、これは誤植だと思い、岩波書店にメールを送った。
メールを送ってなんと6時間後に返事が来たのにはびっくりした。
さすが岩波書店。すばやい対応に感心するばかり。
今回のブログは、私が誤植を見つけた、というだけの内容になってしまったが、この「円周率が歩んだ道」であらためて和算のおもしろさに気づいた。
いつか和算による円周率の計算について勉強したことをこのブログに書いてみたいと思うが、先人の成果を自分のものにするのにはまだまだ時間がかかりそう。
今回は、岩波書店の素早い対応と、江戸時代の建部賢弘などの和算家の素晴らしさに感動したの巻でした。