3月14日は円周率の日
ホワイトデーとも言われているが、円周率の日だと言うことももおぼえておこう。
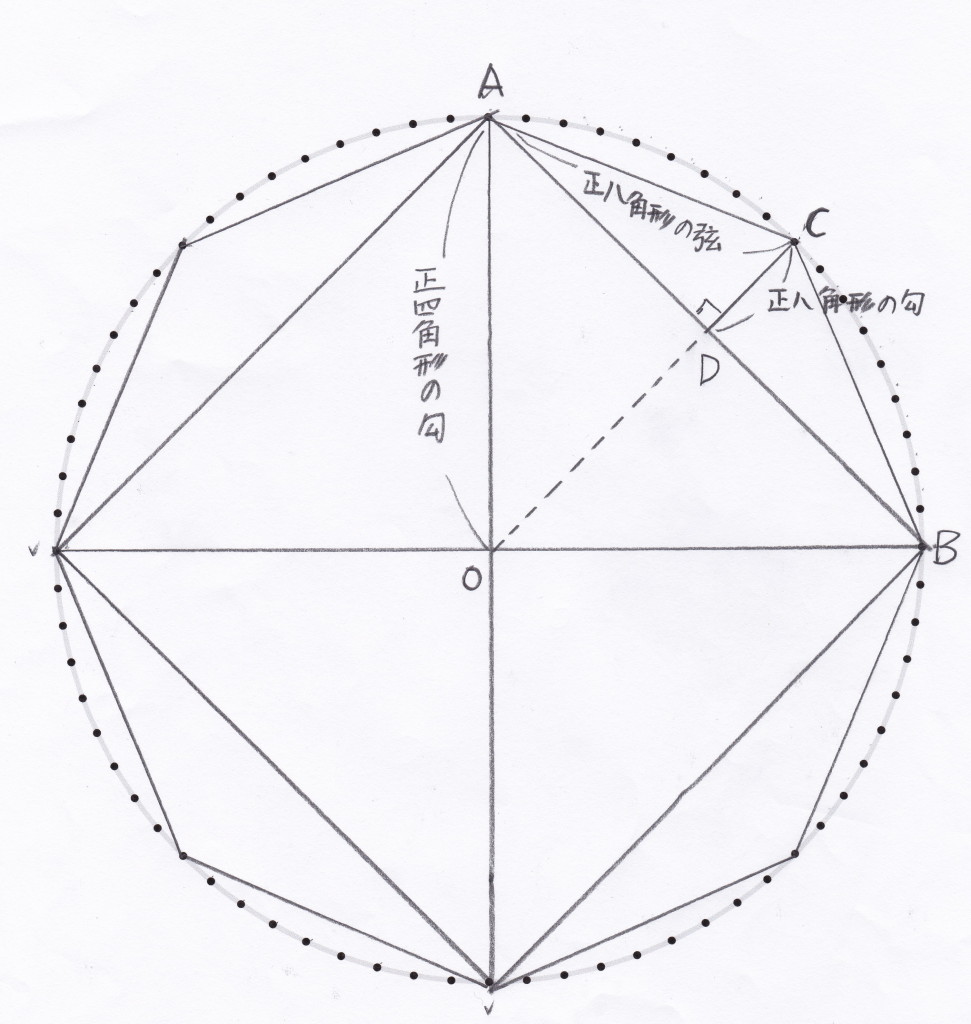
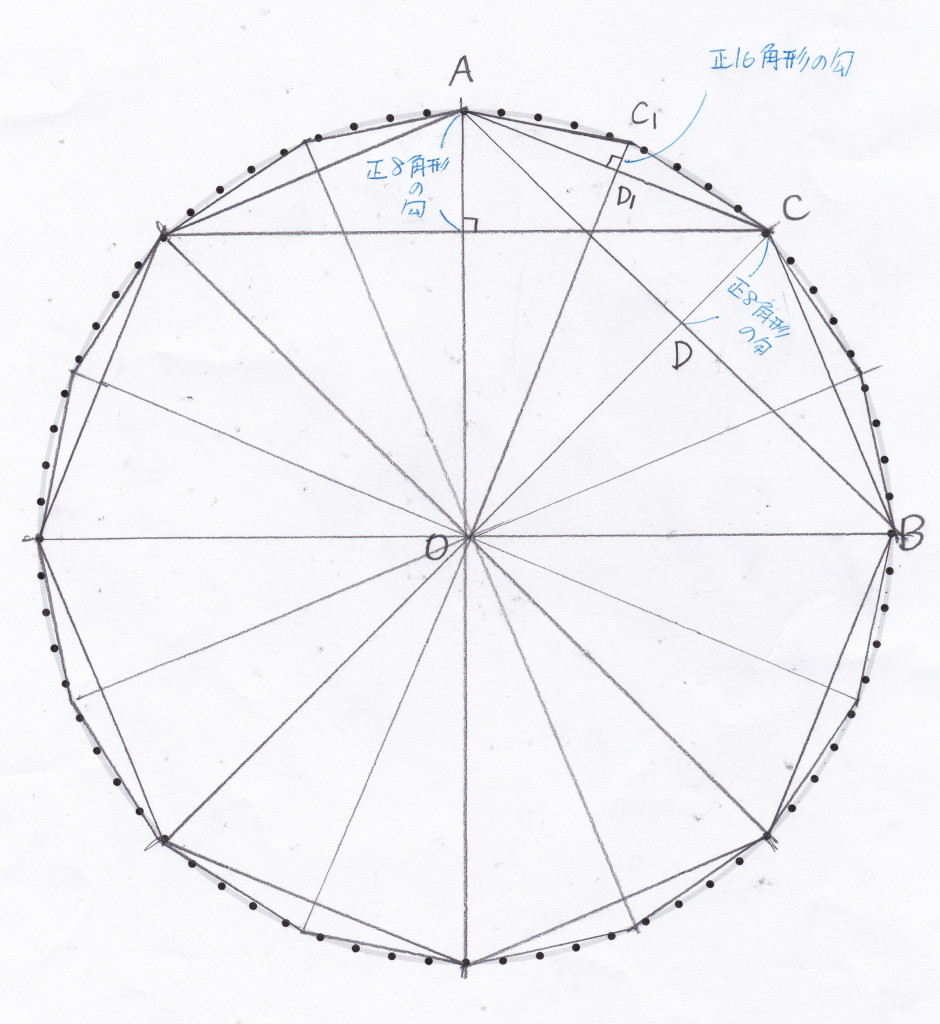
このブログで以前に村松茂清の計算方法を紹介した。 それは円に内接する多角形を考え、三平方の定理(和算では勾股弦の定理)を使って正多角形の周の長さを計算することによって、円周率に接近していく方法だった。
下に簡単に考え方と表計算ソフトによる結果を再掲しておく。
関孝和の方法 3.14159265359微弱
関孝和の計算を調べてみた。 ネットには多くの記事がアップされている。それらを読んだり、本で調べてみて私が理解できた範囲で紹介してみる。
ウィキペディアによると、
「暦の作成にあたって円周率の近似値が必要になったため、1681年頃に正131072角形を使って小数第11位まで算出した。関が最終的に採用した近似値は「3.14159265359微弱だったが、エイトケンのΔ2乗加速法を用いた途中計算では小数点以下第16位まで正確に求めている」とある。
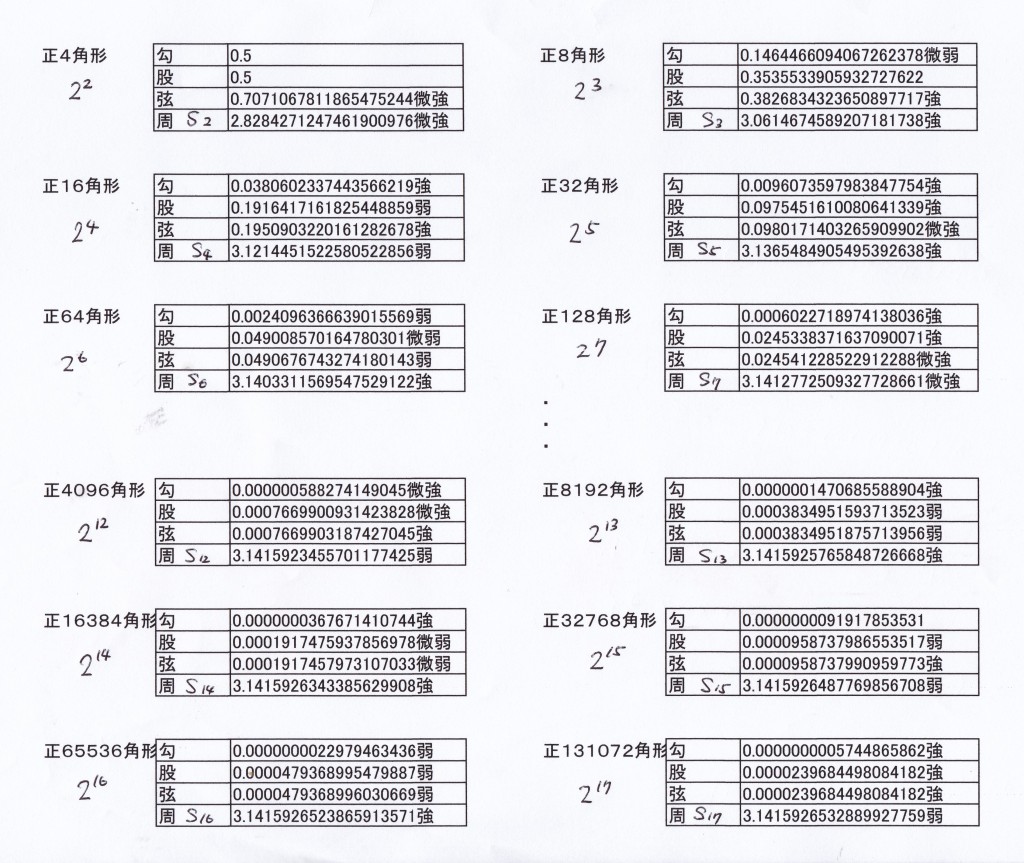
関孝和も村松茂清と同じように計算をしている。ウィキペディアにあるように、正131072(2の17乗)角形を使っている。なんと小数点以下19桁までの数値がだされている。
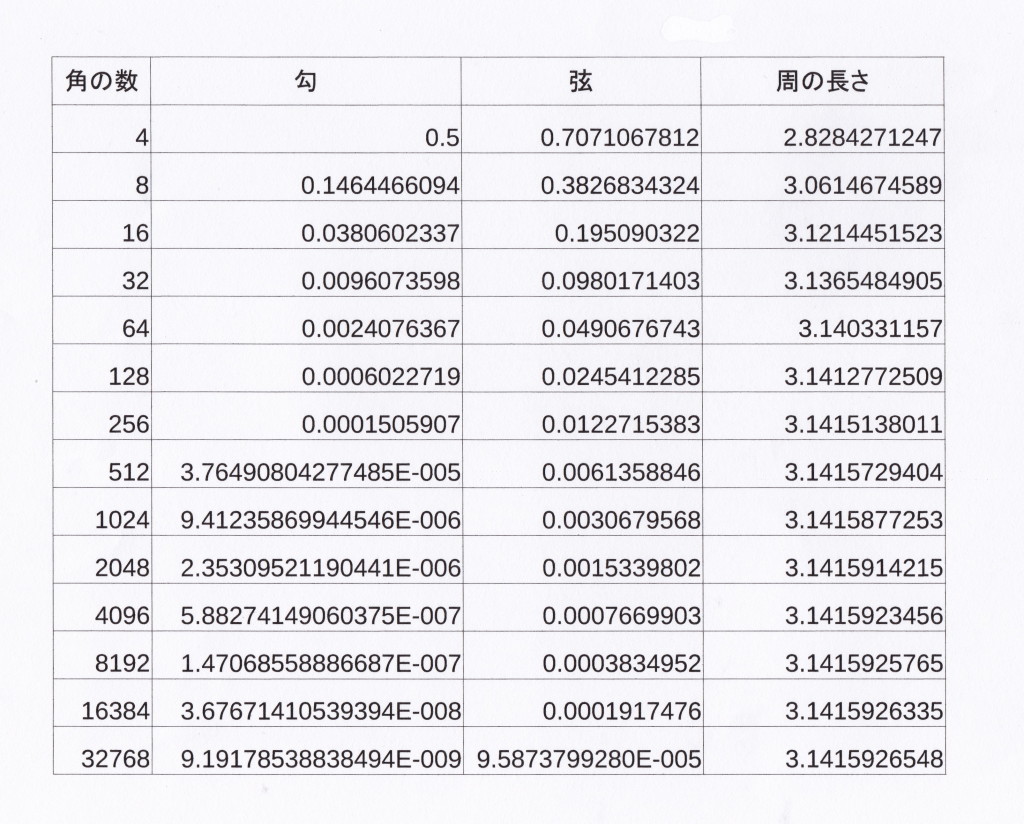
(Excelなどの表計算ソフトは12桁以上の数字を表記することはできないので,記号として入力して表にしたものが下の表である。)
(表をクリックすると拡大像になる)
(表にある強、弱について。 四捨五入により切り捨てた場合が強。切り上げた場合が弱。とくに末位が0を切り捨てた場合は微強。末位が9を切り上げた場合は微弱である。)
関孝和はこの円周の長さの変化に着目したようだ。
さて、このような式はどうして導かれたのだろうか。
関孝和の素晴らしいと言われているのは、円周率を求める一般式を考え出そうとしたところだと思う。
村松茂清のような方法は、円周率を力づくで何桁でも計算できるだろう。しかし、この方法はあくまでも近似値を求めているのであって、最終的に円周率はどうなるの?という疑問には答えていない。
わたしの分かる範囲で説明を試みてみる。
ここまでの説明は、関孝和は等比級数を使って円周率の計算をしたのだろうという推測のもとで、なされている。 本当に等比級数を使ったのかどうか?それは確証がないそうだ。 それ以外の方法で式を導いたという説もある。
関孝和が実際には等比級数の考え方を使ったの、あるいは差分に注目して計算式を導き出したのか?それはわからない。
江戸時代の和算の本の多くは、結果のみが記されていて、その考え方や計算方法がのせられていないそうだ。
この式も弟子の建部賢弘や後世の数学者たちが研究し、資料として記されているので私たちが学ぶことができるのである。
いずれの方法にしても、関孝和の時代にこれほど精密に円周率を求めたものはいないと言われている。数字の向こうにある世界を探求しようとした熱意に敬服するしかない。
(2015年3月14日 円周率の日に記す)