スクラッチを使って円周率を求める
 「子供の科学」11月号の付録に「円周率10000ケタ」の付録がついていたことは前回に紹介した。
「子供の科学」11月号の付録に「円周率10000ケタ」の付録がついていたことは前回に紹介した。
12月号の記事に「スクラッチをつかって円周率を求める」内容の記事があった。
円周率をパソコンで求めるには、それなりの準備や工夫が必要だ。
ずっと昔に、ベーシックで計算をすることを経験したが、なかなかの苦労だった思い出がある。
「子供の科学」にあるスクラッチは最近の小学校のプログラミングの体験にも使われているというもので、かつて私がベーシックを触った時のアルファベットと数字をタイピングして入力したものではなく、もっとビジュアルのものだった。
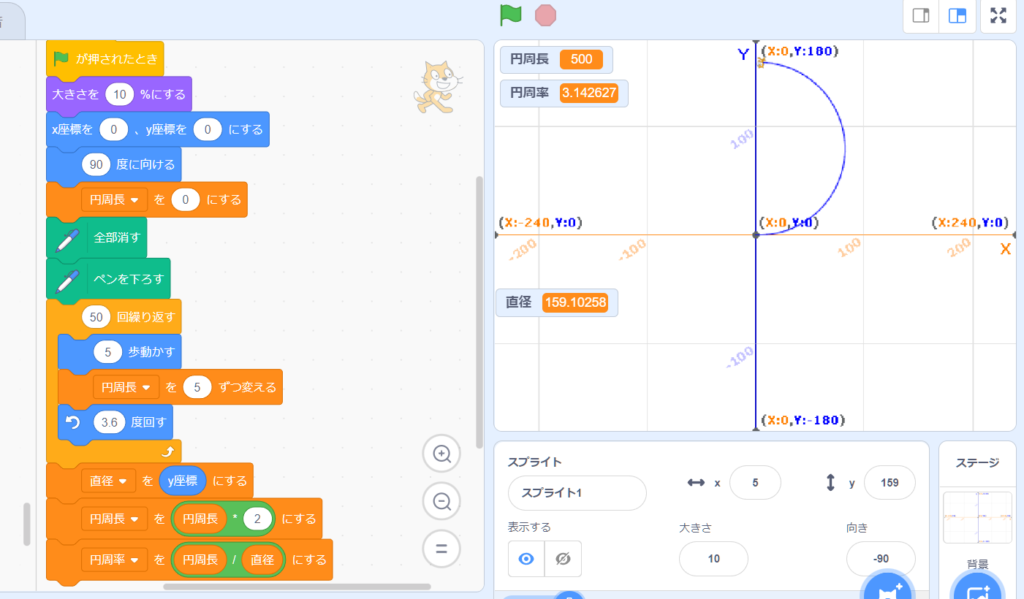
上の写真が私が入力して動作させた結果の画面の一部。
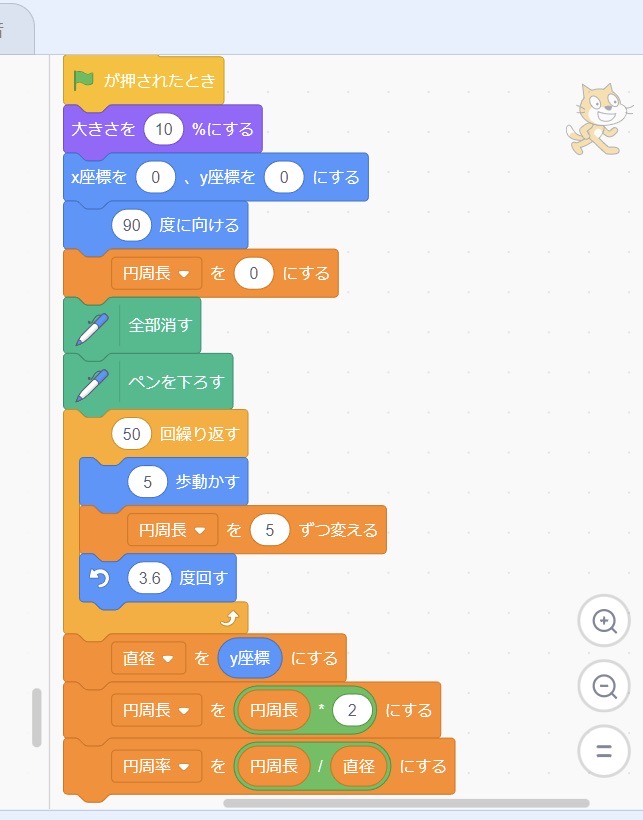
これがプログラムの全容。
最初の「大きさを10%にする」というのは猫の大きさを10%に縮小するというもの。
次にx座標とy座標を0にし、90度に向ける、というのは「スタート地点はステージの中央(0.0)で、右(90度)向いている状態にする、ということ。
次に円周の長さを「円周長」という変数にして、初期化(0)にしておく。
ペンを使って図をかけるようにする。
初期化するために「全部消す」とし、次に「ペンを下ろす」と書く準備をする。
円を一周かくというのは、ステージ上の猫を360度動かすことである。
これを100角形の図を書くと捉え直し、
360 / 100 = 3.6
まわす角度を3.6 にすればいいことがわかる。
歩数を5歩にしているのは、10歩にするとステージをはみ出すからである。
100回繰り返すと全周になる。
ここで直径を出すための工夫として、半周の時の「y座標」の値を利用する。
半周というのは、50回くりかえし、そのときのy座標の値が丁度直径の長さになるからである。
円周は変数「円周長」を利用する。
歩数が一辺の長さなのでそれを足し算すればよい。ここでは半周だからそれを2倍すれば円周の長さとなる。
これらをすべてスクラッチのプログラムで書くと上の図のようになる。
15行ほどのプログラムだから私はびっくりした。
ベーシックでは何十行にもなるプログラムをキーボードで叩き込んだことを思い出すと、雲泥の差だ。
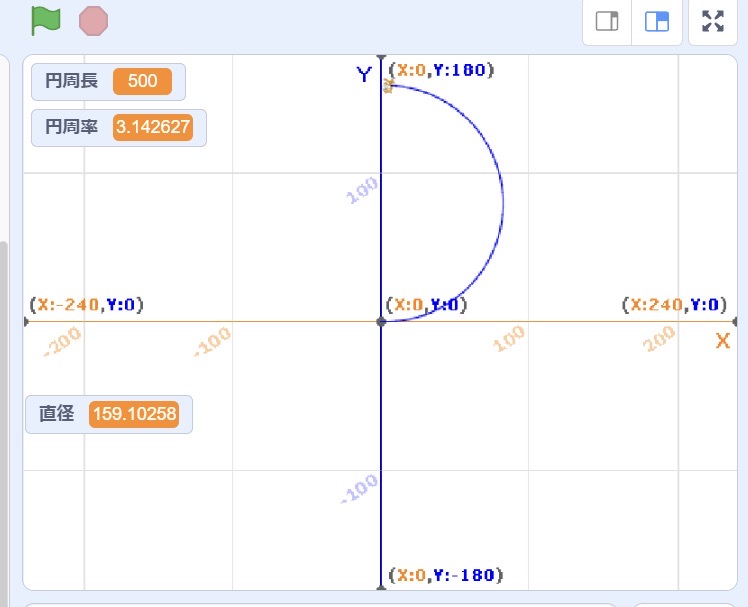
上の写真はステージ上の円と円周率などの表示の部分。
円周は5歩が100回だから円周長は500になる。
直径は図のy座標の値。スクラッチの計算では 159.10258
そして円周率は 円周/直径 だから
159.10258 / 500 = 3.142627
実際は 3.141592 だからなかなかいい数字ではないか。
このスクラッチのプログラムは正100角形をかいているが、
これを1万角形などにすれば、もっと正確な円周率が計算されることが予想されるが、今回はここまでとしよう。
「子供の科学」の記事は本当に役に立った。ここで感謝申し上げる。