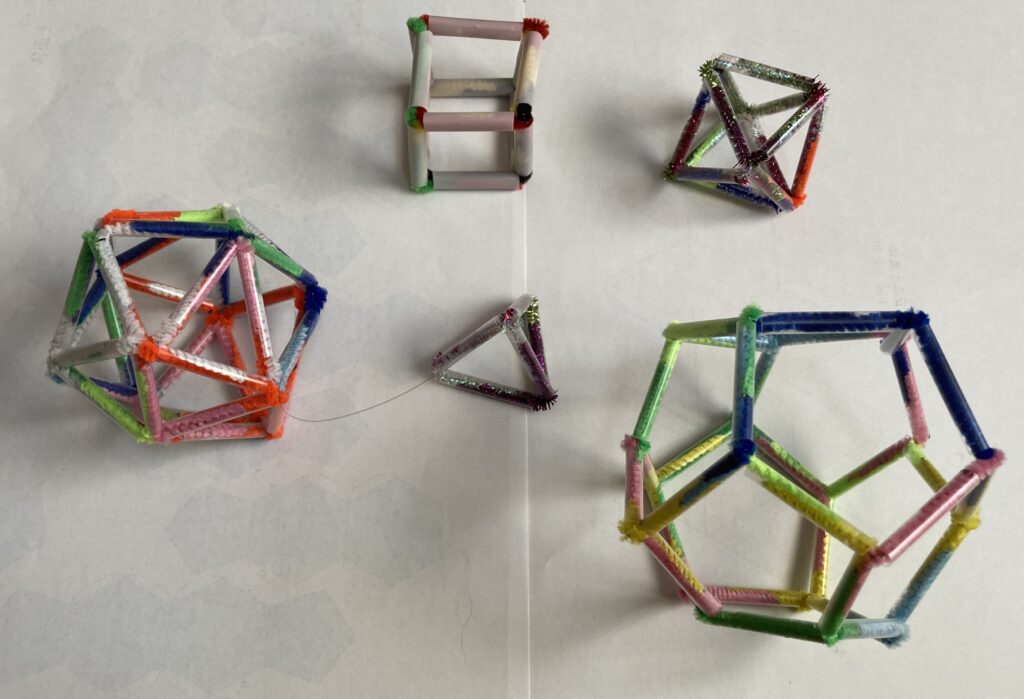多角形で囲まれた立体を多面体という。その中でも一種類の正多角形の面で作られたものを「正多面体」とよんでいる。
正多面体は、正４面体・正６面体・正８面体・正１２面体・正２０面体の五種類しかない。
プラトン（紀元前４２７〜紀元前３４７）が著書「ティマイオス」で正多面体についてふれているので、正多面体は「プラトンの立体」とも呼ばれている。
（参考同志社中学校のホームページより）

正多面体を紙で作ったのが一番上の写真。
正多面体の頂点や辺の数などを調べるには、左のようなモールを使った正多面体の立体模型が便利だ。
左のモールによる正多面体の模型は、「ストローとモールでつくる幾何学オブジェ　１００均グッズで学ぶ多面体」（日本数学検定協会　丸善出版株式会社）の本によって作った。
この本で紹介されているように、１００均で売っているストローとモールさえあれば、プラトンの立体を作ることができる。

上の写真がストローとモールで作った正多面体５種類。
１００均では色のついたストローと無色透明のストローが売っていたが、模型としては透明ストローのほうがモールの色がわかってカラフルだ。

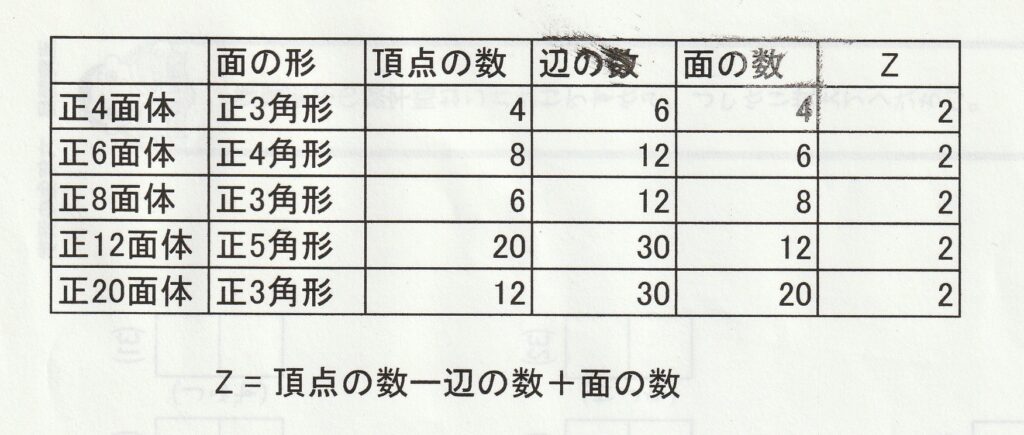
この本に、正多面体の頂点の数や辺の数を調べてみようという課題があった。
それが上の表。
頂点の数、辺の数、面の数の関係を調べてみると、

頂点の数から辺の数を引き、面の数をプラスするとすべて２になることがわかる。

この関係は「オイラーの多面体定理」とよばれているものだ。

今回私は正多角形を作り、そこから正多面体に発展していった。
そして「正多面体は、正４面体・正６面体・正８面体・正１２面体・正２０面体の五種類しかない。」とか「正多面体の頂点の数、辺の数、面の数には、Eulerの多面体定理とよばれる関係がある」ことがわかった。
なぜ正多面体には５種類しかないのか、なぜオイラーの多面体定理が成立するのかについては、ネットで検索すると多くの証明や説明が紹介されていることがわかる。
そういうことでここではその説明は省くことにする。興味のある方は是非ネットで検索することをおすすめする。

上の写真は正１２面体と正２０面体のち地球儀の模型。
これは
「発見・体験！　地球儀の魅力　地球儀を自作しよう！」（稲葉茂勝著　少年写真新聞社）
の本にある地球儀の模型の展開図をもとにしてつくったもの。
球形の地球儀を紙で作ったことはあるが、写真のような正多角形をもとにした地球儀は初めてだった。球体を作るのはむずかしいが、多面体なら少しなんとか作れそう。しかし糊付けに手間がかかり苦労したが、やってみると楽しい作業だった。