3×3×3ソーマ・キューブ
今回作ったのは「3✕3✕3ソーマ・キュープ」。

参考にしたのは「Play Puzzle パズルの百科」(高木茂男著・平凡社)。
この本によると
「デンマークの詩人で、数学ゲーム考案家でもあるピェット・ハインが創案したもの。
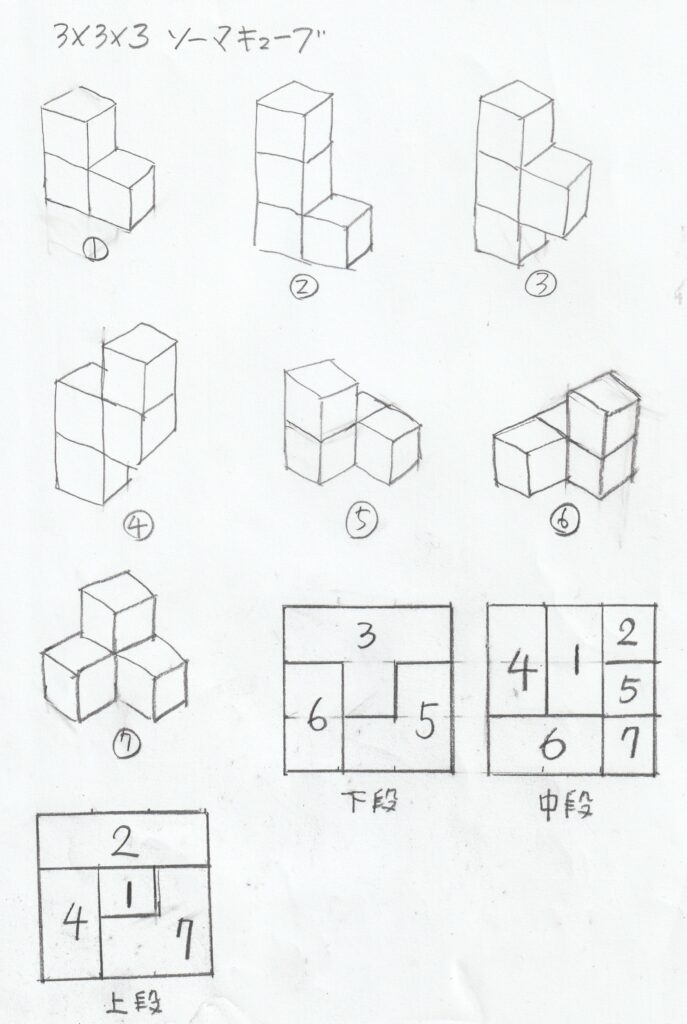
4個以下の立方体を面と面とではりあわせてできる立体のうち、どこかに出っ張りや引っ込みのあるものだけを選ぶと7種類のものが得られる。これを全部つかつて立方体を作るのが、ソーマ・キュープである。
これはヨーロッパでも、アメリカでも、日本でも用具が売られ、キューブ・パズルの中ではもっともポピュラーなものである。立方体以外にも、いろいろな形を組む遊び方がある」
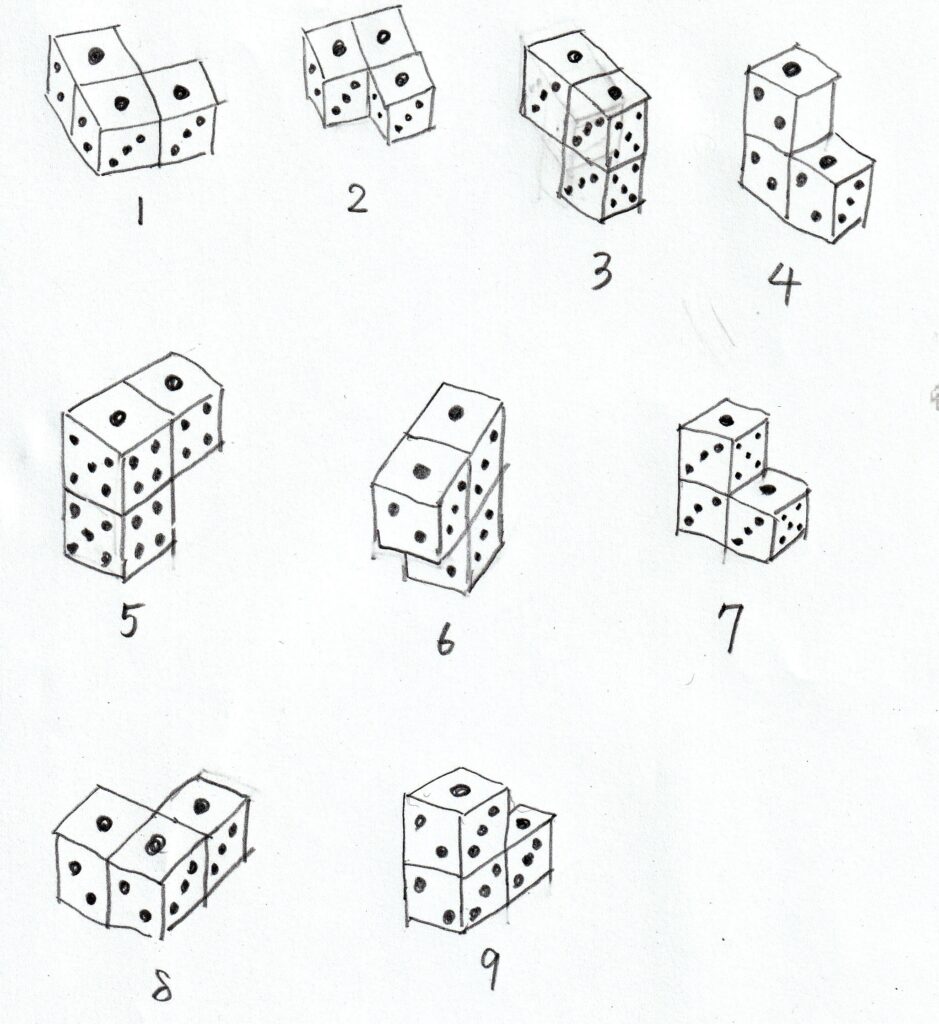
図からわかるように、立方体3個のものが1つ(番号①)で、あとは4個の立方体からできている(番号②から⑦)。
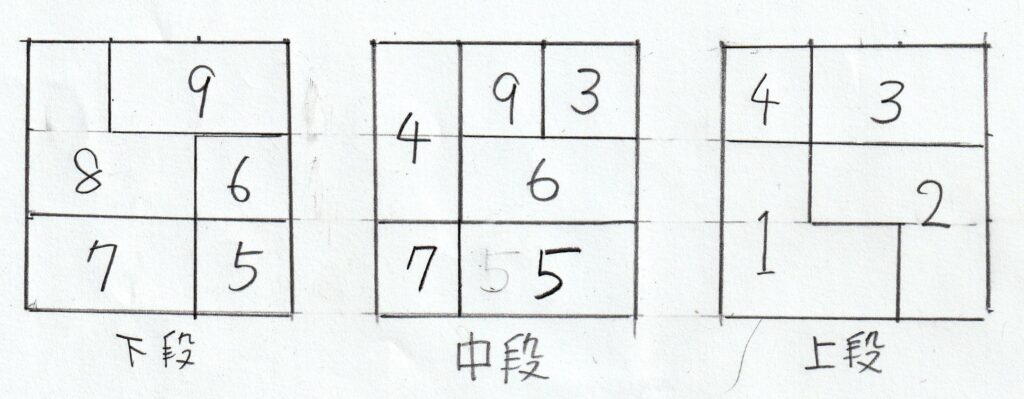
立方体に組み立てるのは、図のように下段・中段・上段と組み合わせを考えて置いていく。
上の写真左が下段の様子、右が中段の様子である。
そして上段はトップの写真のようになる。
ウィキペディアによると、
・・・・・・・・・・・
「Piet Hein はこのパズルをヴェルナー・ハイゼンベルクの量子力学の講義中に考えた。
ソーマの名称の由来は諸説あり、オルダス・ハックレーの小説「Brave New World」に登場する架空の薬に由来するとも、その元となった神話上に登場するソーマに由来するともいわれている。・・・後半略・・・・
立方体に組む方法は、なんと240通りもあるそうだ。
上の写真はそのうちの1つ。
ウィキペディアによるとこの240通りのパターンがのった本があるという。
原題は Winning Ways for your Mathematical Plays.
邦題は「数学じかけのパズルゲーム」だそうだが、どんな本なのか私はまだ見たことがない。