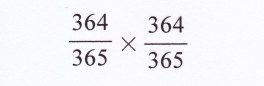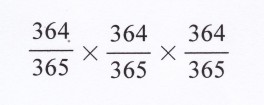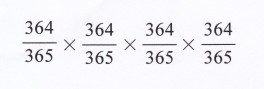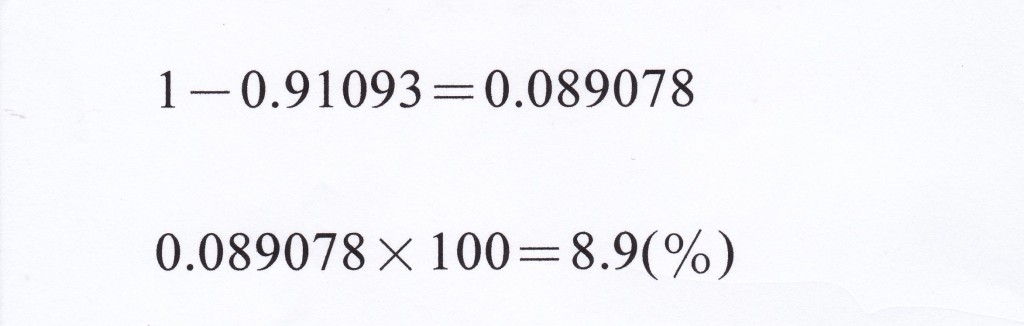自分と同じ誕生日の人がいる確率は?
35人の集団があるとする。自分と同じ誕生日の人がいる確率はどれくらいなのだろうか。
計算してみよう。
まず2人の場合。A(1)さんとA(2)さんがいるとする。
A(2)さんがA(1)さんの誕生日と違う確率は、
364/365
である。(一年は365日の平年として)
A(3)がやってきて、その人がA(1)さんの誕生日と違う確率はやはり
364/365
である。
A(1)さんと違っていればよいのであってA(1)さん以外の人の誕生日が同じだろうが違っていようが関係ない。したがって3人の場合でA(1)さんの誕生日と一致しない確率は、
同様にしてA(4)さんがやってきて、この人がA(1)さんと誕生日が違う場合を考えると、やはりその確率は
364/365だから
3人の誕生日がA(1)さんと違う確率は、次のようになる。
次にA(5) さんがやってきて5人の場合を考えると、その人がA(1)さんと誕生日が同じにならない確率は、364/365。
4人がA(1) さんと違う誕生日になる確率は、これまでと同様に考えて、
となることがわかる。
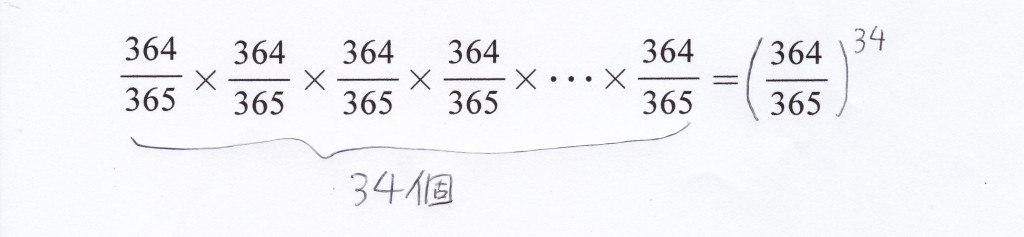
このようにして考えると、A(2)さんからA(35)さんまでの誕生日が、A(1)さんと違っている確率( A(1)さん以外の人の誕生日は重なっても、重ならなかっても関係ない ) は、次のようになる。
この計算をしてみよう。前回のように累乗を計算するサイトを利用すると、

この結果は、35人のクラスでA(1)さんの誕生日と違う人がいる確率。
求めたいのは「自分と同じ誕生日の人がいる確率」だから、1から上の結果を引けばよい。
約9%の確率で、自分と同じ誕生日の人がいる。逆に言えば、35人いれば91%の確率で、自分と同じ誕生日の人がいない! ということになる。
35人いれば、自分の誕生日と同じ誕生日を持つ人がいる確率は約10%、約1割しかいない、9割はいない、という結果はなんとなく実感に近い、となるのではないだろうか。
日付を指定してその日の誕生日の人がいる確率は
それでは35人の人がいて、1月1日生まれの人がいる確率は? のように、日付を指定してその誕生日の人がいる確率を求めてみよう。 1年が365日の平年として考えると、 1年でその日になる確率は1/365だから これまで計算してきた値に1/365を掛ければいいことになる。
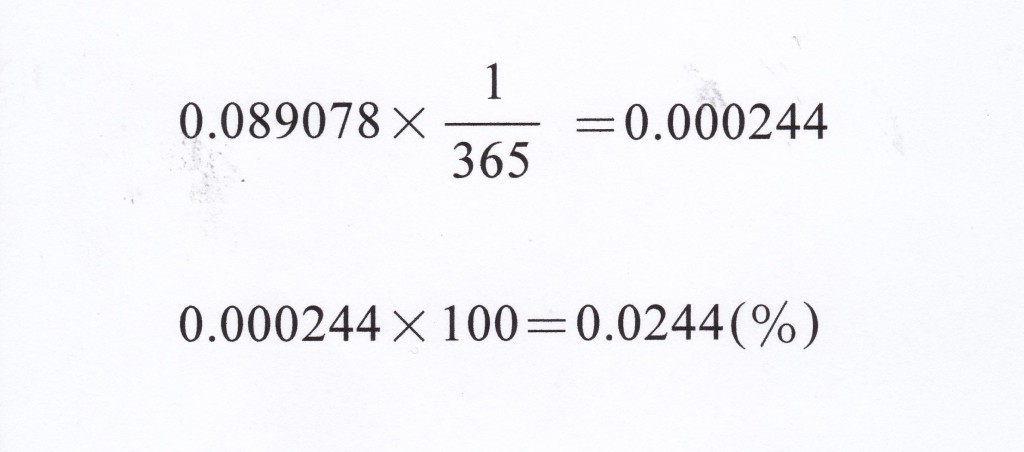 35人の学級があったとしたら、そのクラスで、例えば1月1日生まれの人がいる確率は、
35人の学級があったとしたら、そのクラスで、例えば1月1日生まれの人がいる確率は、
0.000244 ⇒ 0.0244%
ということだから、極端に少ないことがわかるし、これも実感にちかいものだと思う。
ある集団があってそのなかで「だれでもいいから誕生日が同じ人がいる確率は?」を考え、次にその集団で「自分の誕生日と同じ人がいる確率は?」考えてきた。そして最後には「ある決まった月日の誕生日の人がいる確率」も考えてきた。
タイトルに「バースデイクライシス」としてきたが、何が「クライシス」(危機)なんだろう?
その説明は次の機会に。