同じ誕生日の確率
さて前回は、35人のクラスで同じ誕生日の人がいる確率を求める式を考えた。
左がその式である。
!は階乗の計算をする、という意味で、たとえば10!(10の階乗)は、
10!=10✕9✕8✕7✕6✕5✕4✕3✕2✕1
の計算のこと。
ここでは365の階乗だから、
365✕364✕363・・・✕2✕1
という365回の掛け算をすることになる。
いったいどれくらいの数字になるのだろう。それがこれ。
2510412867555873229292944374881202770516552026987607976687259519390110
6138220937419666018009000254169376172314360982328660708071123369979853
4453679106538723835997043555327409376780914914294408643160469250745101
3484702554601409800590796554104119549610531188617337343514551719328276
0847755882291690213539123479186274701519396808504940722607033001246328
3988005504874279998766904169734378610781853446679668715110496538881301
3683619901052918005612584454948864861768291582634756414899098413806780
9999604687488146734837340699359838791124995957584538873616661533093253
5512568450560463887381297029513811518614136889229865100054409439430146
9924411255575527914076049276425374025041039105642197900328960000000000
0000000000000000000000000000000000000000000000000000000000000000000000
000000000
この答えは, 779ケタの数で末尾に0は89個連続する。
これはインターネット上に階乗の計算をしてくれるサイトがあったのでそれを利用した。http://www.kishimo.com/math/kaijou.html
同様に365の35乗をを計算すると、
4789059755391665870080907767022554796790253476056121056776945923251332
71515369415283203125
となる。これもネット上のサイトを利用した。http://www.kishimo.com/math/ruijou.html
これらの数字を代入して紙と鉛筆で計算することは、私の力では果てしもなく時間がかかりそう。電卓でもこんな桁数の多い計算はできない。
Excelに代入しても受け付けてくれない。
ここは先人の力に頼って、その努力の結果を紹介する。
この表は前回紹介した本「社会にも法則はあるか」(仮説社)に載せられている。
この表より、
この計算結果より、 35人いるクラス・集団では、同じ誕生日の人がいる確率は
0.8144になった。%でいうと約81.5%であることがわかる(切り上げている)。
そうすると、たいていの学級では8割の確率で同じ誕生日の人がいることになる。
へえー、そんなに高い確率だったのか、と驚く数字だ。
人数が多いほどその確率が高くなることは予想できる。
計算して表にまとめてみると(これも紹介した本の資料より)。
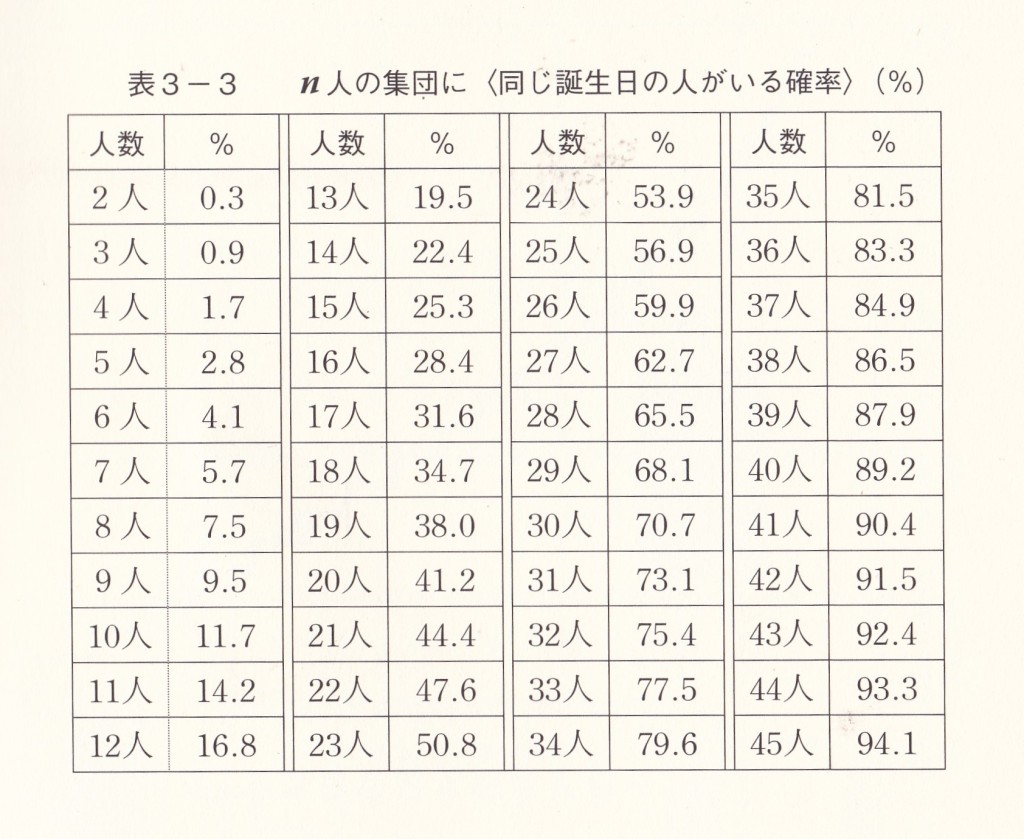 40人をこえると9割の確率で同じ誕生日の人がいることが分かる。
40人をこえると9割の確率で同じ誕生日の人がいることが分かる。
どれくらいで5割の確率となるのだろう? 表を見ると23人を超えると確率が5割をこえている。
この表をグラフ化したものも、この本には載せられている。
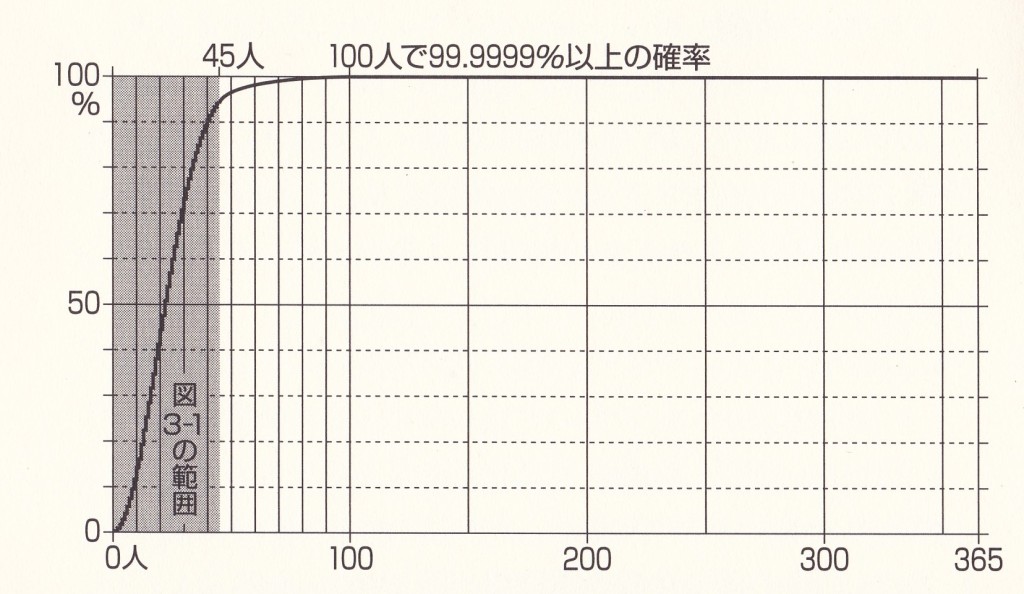 100人では99.9999以上の確率で同じ誕生日の人がいることが予想される。つまり人が100人以上いれば、同じ誕生日の人はほぼ確実にいてるということだ。
100人では99.9999以上の確率で同じ誕生日の人がいることが予想される。つまり人が100人以上いれば、同じ誕生日の人はほぼ確実にいてるということだ。
へーっ、と驚くとともに何か腑に落ちないところがある。35人で8割だなんて……という気持ち。
実はその気持は「自分の誕生日と同じ人がいる確率」とごっちゃにしているからである。
今計算したのは「35人いれば誰か、だれでもいい、誕生日が同じ人がいる確率は8割」であって、自分の誕生日と同じ人がいる確率が8割というわけではない。
では、自分と同じ誕生日の人がいる確率はいくらほどになるのだろうか。
このことは次回に考えてみたい。
*引用した資料は、「社会にも法則はあるか 誕生日をめぐる法則」(仮説社)より。

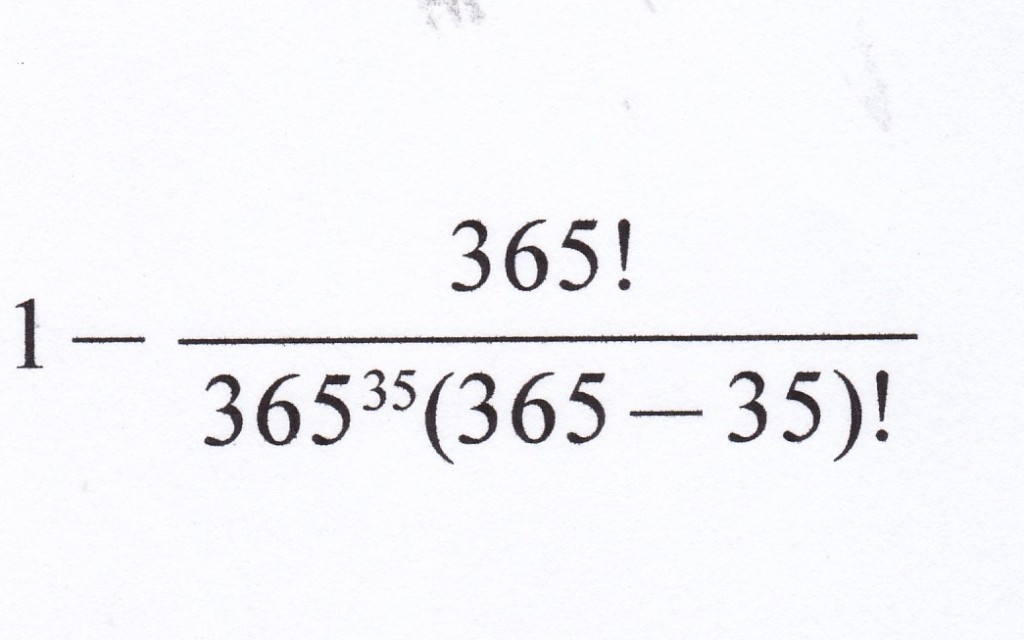

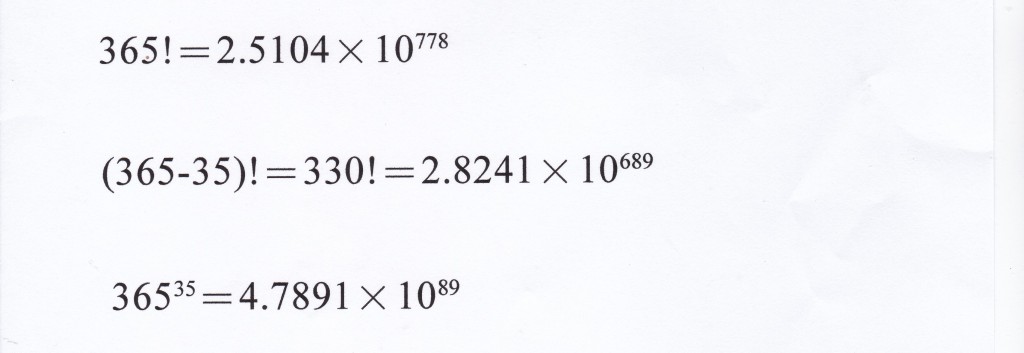

金曜日の米寿の会のお世話有り難うございました。パソコンのメールに写真の件を送りました。
誕生日が一緒の人はあまりいませんね。でも、病院で血液検査をする時に「誕生日が同じ人がいるので生年月日をお願いします」と毎回言われます。少なくともその病院に通っている人の中に同じ誕生日の人がいるようです。次回の同じ誕生日の確率は楽しみです。
生年月日と血液型を聞くんですか。それは初耳です。
この情報を私のブログで使わしてくださいね。
バースデイクライシスを予防する方法に使えそうです。
バースデイクライシスとは何か、お楽しみにしてください。