「算俎」村松重清の方法
今回は、江戸時代の和算家の方法を追跡してみよう。 「円周率が歩んだ道」(岩波現代全書 上野健爾著)によると、「円周率の計算を記した初期の書物としては、村松重清著『算俎』(さんそ)である。村松重清の婿養子であった村松秀直は赤穂浪士四十七士の一人である。村松は『算俎』のなかで円に内接する正多角形の周の長さを計算して円周率の近似値を求めた。彼は直径一尺の円に内接する正8角形から始めて正32768(2の15乗)角形の周の長さを計算して3尺1寸4分1592648776..を得た。これは小数点以下7桁まで正確な値をあたえている..」とある。
この方法を追試してみよう。
まず江戸時代の三平方の定理は鉤股弦(こうこげん)の法(勾股弦とも書く)とよばれていた。
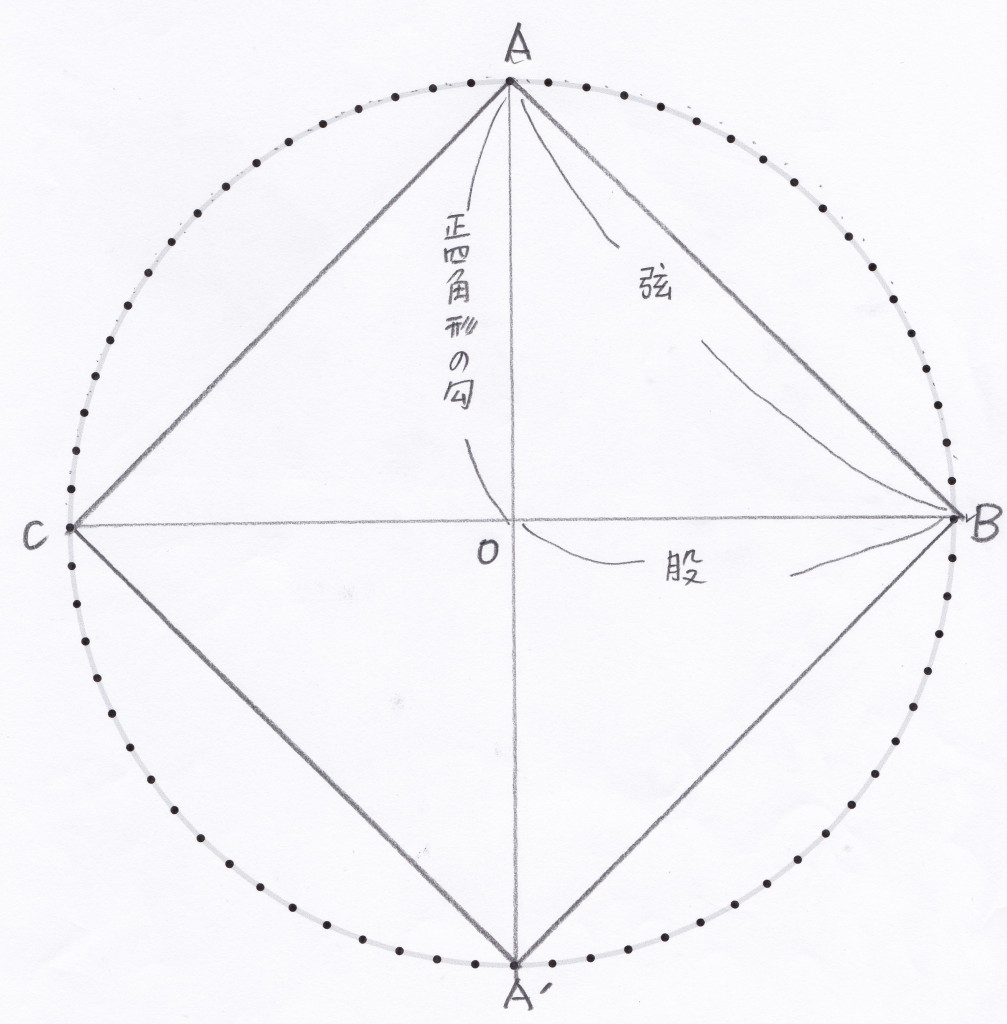
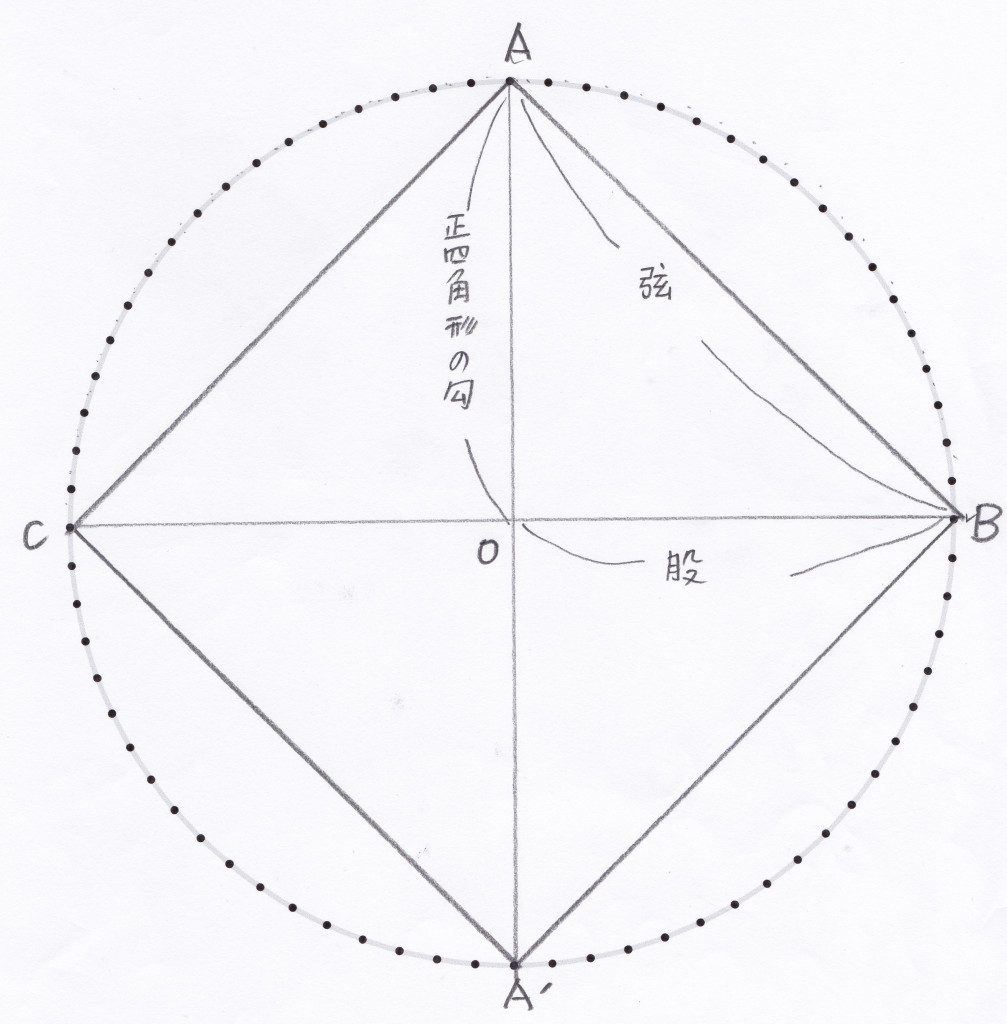
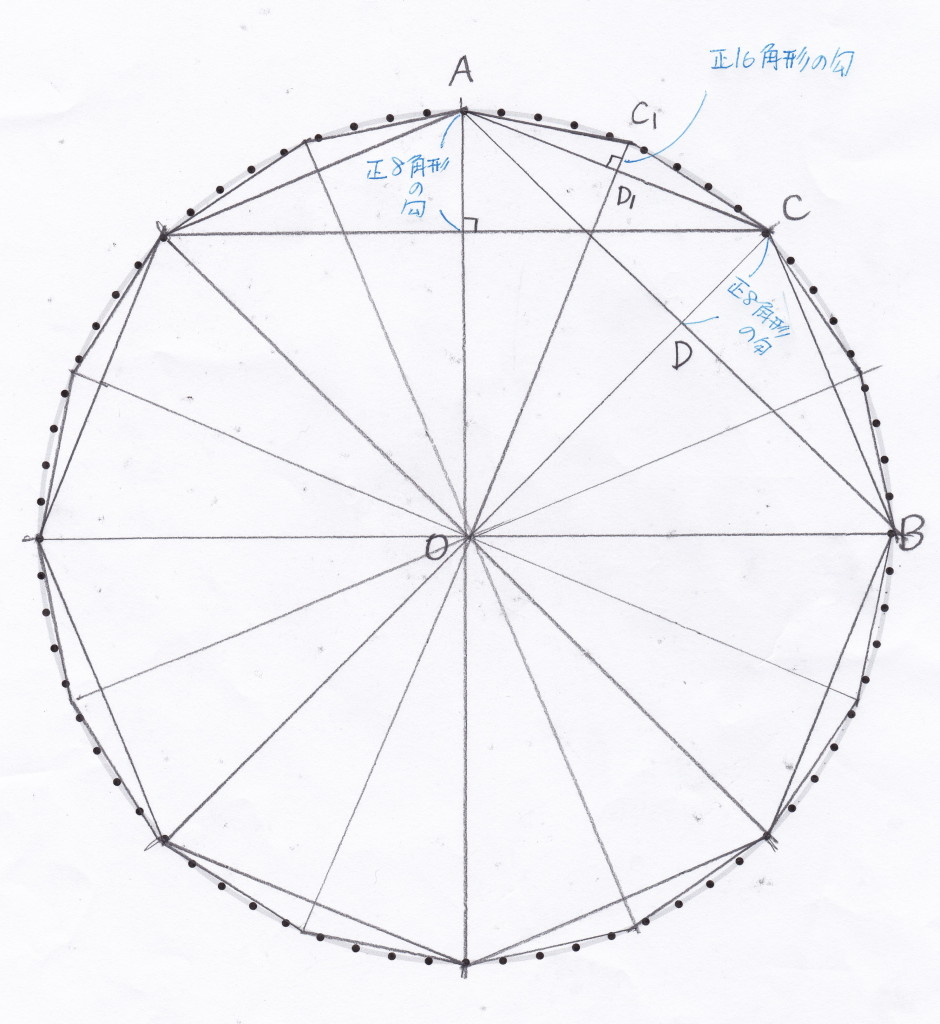
直径1(単位は省略)の円に内接する多角形、ということなので四角形からスタートする。まず準備段階として、弦と勾の関係を調べておく。
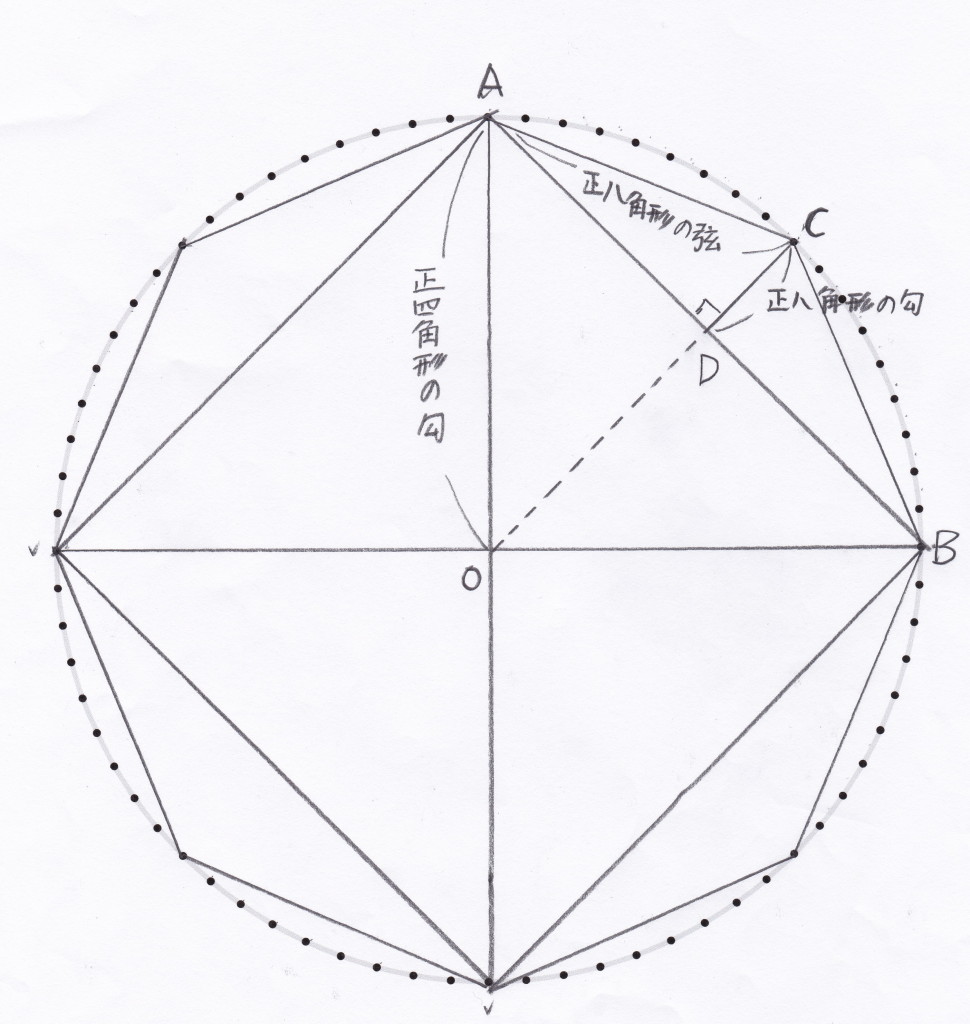
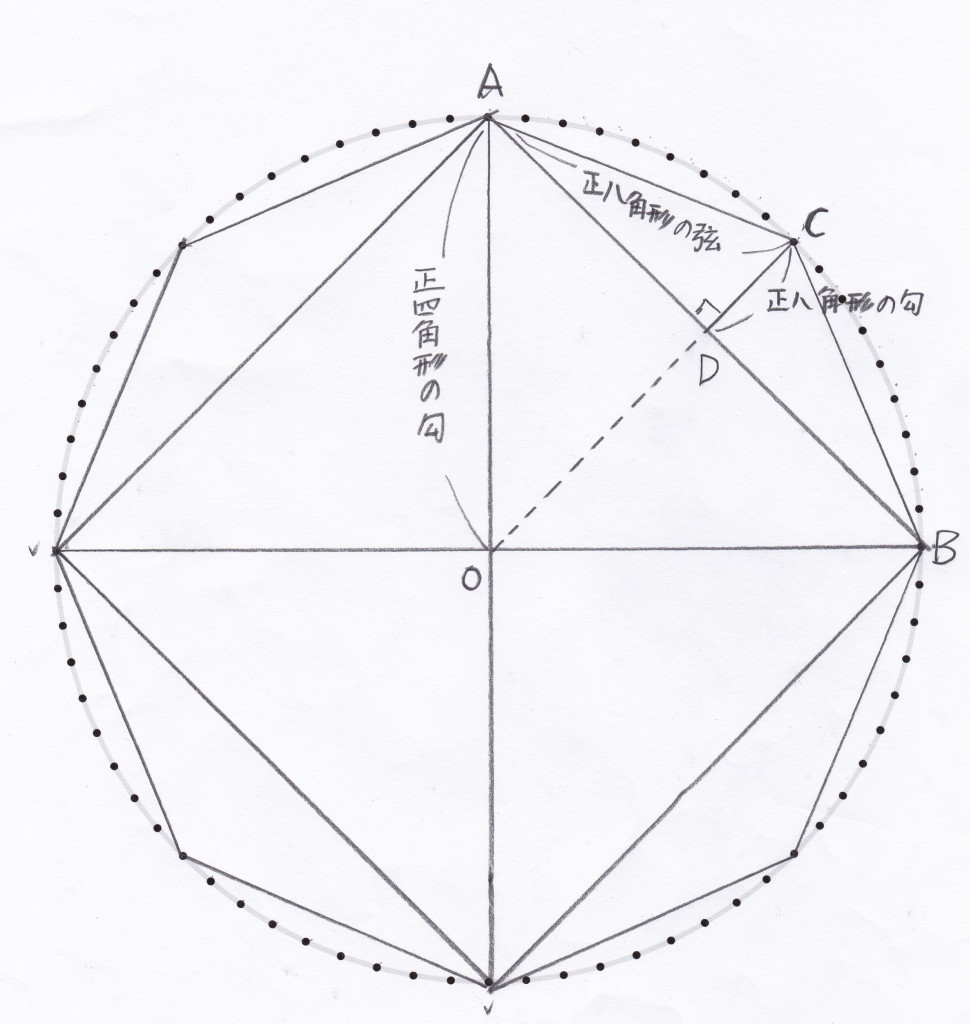
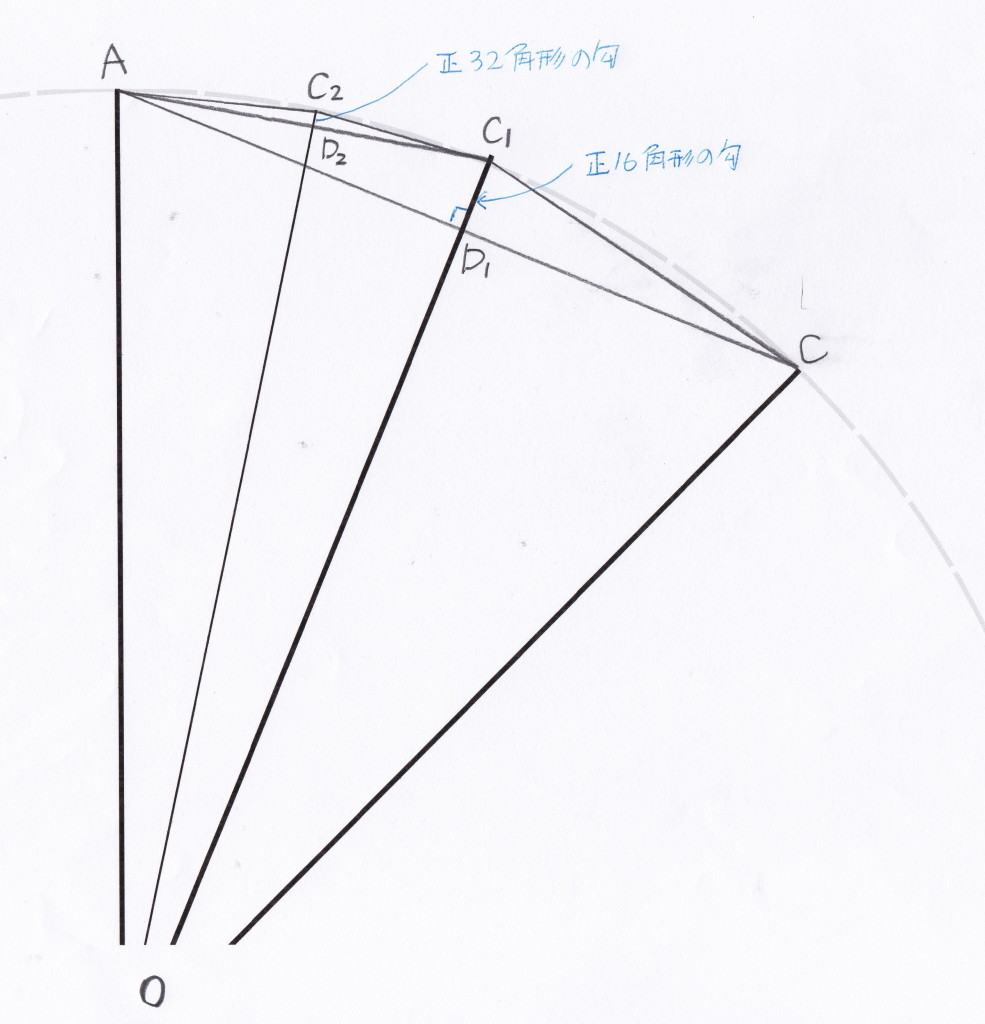
さらに分割してみる。
4角形の場合
8角形の場合
16角形の場合
32角形の場合
ここまでくると、この弦と勾の関係はこのまま思考実験で継続しても大丈夫。
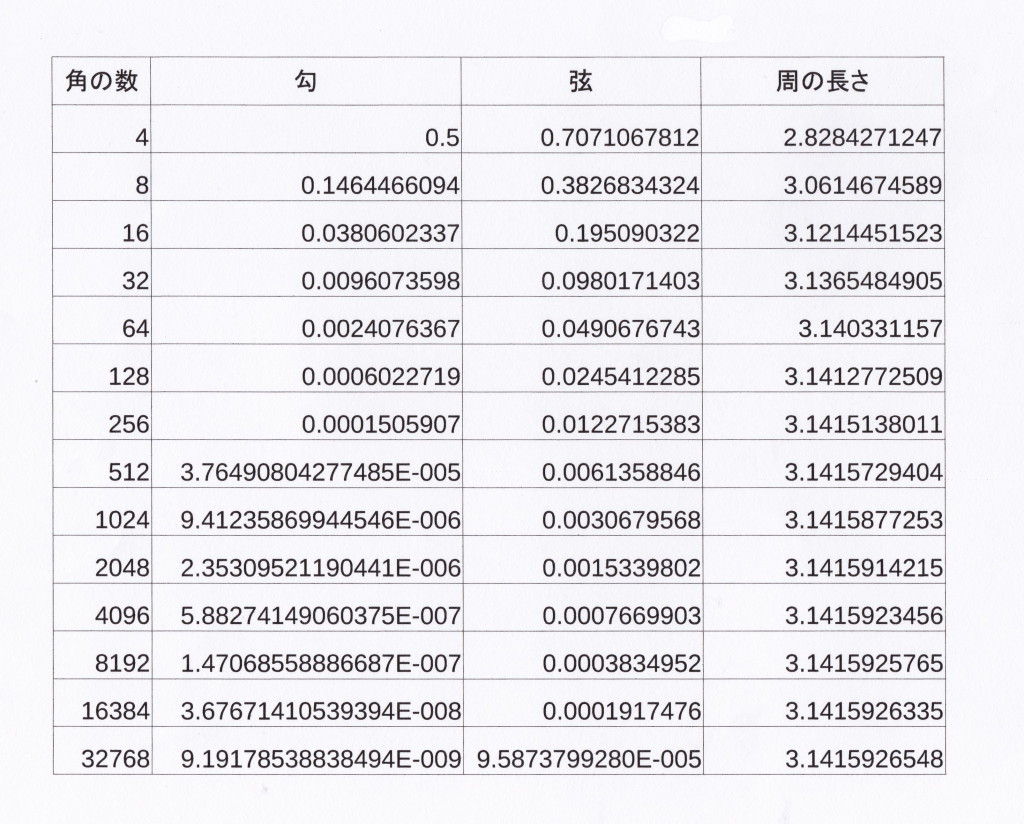
村松重清が計算した正32768角形までを一覧表にしてみたのが次の図。
表計算ソフトで計算してみよう。

関数を使った計算は表計算ソフトの得意とする所。前回はエクセルを使ったが、今回は無料ソフトのLibreOfficeを使った。
計算した結果がこれ。
直径を1としているので、円周の長さが円周率となる。
村松重清は正32768角形の辺の長さで円周の近似値を計算し、それが円周率と等しい、という考えをここまで実行した。
村松重清の計算は、3尺1寸4分1592648776..で、表計算ソフトよりも多くの桁数まで求めている。
その集中力と計算の確かさに驚く。
そろばんによって計算したと思うが、どれほどの時間がかかったのだろう。
私たちは円周率の値を知っているから、計算間違いに気づくことはできるが、正解がわからないなかでここまで正確に計算されていることに驚くばかりだ。